Chỉ cần đáp án thôi ạ
cho hình chóp S.ANCD có đáy ANCD là hình bình hành.Bộ ba vecto nào sau đây đồng phẳng?
A. SA,SD,BC
B. SA,SB,AC
C. AB,AC,SD
D. SA,SC,BD
Cho hinh chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng \(\left(\alpha\right)\) cắt SA, SB, SC, SD tại A', B', C', D'. CMR: \(\dfrac{SA}{SA'}+\dfrac{SB}{SB'}=\dfrac{SC}{SC'}+\dfrac{SD}{SD'}\)
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi G là trọng tâm tam giác SAC. Mặt phẳng (a) qua G cắt SA; SB; SC; SD lần lượt tại A'B'C'D'.
1) Tính \(\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}-\dfrac{SD}{SD'}\right)\)
2 ) Tính \(\dfrac{SA}{SA'}+\dfrac{SB}{SB'}+\dfrac{SC}{SC'}+\dfrac{SD}{SD'}\)
Với giả thiết: hình chóp S.ABCD có đáy là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Ta có:
A. MN // (SCD)
B. EF //(SAD)
C. NF // (SAD)
D. IJ //(SAB)
Đáp án D
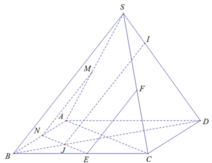
Gọi M là điểm bất kì trên cạnh SA
Trong (SAB), kẻ Mx // SB, Mx cắt AB tại N
Trong (ABCD), kẻ Ny // AC, Ny cắt BC tại E
Ny cắt BD tại J
Trong (SBC), kẻ Ez // SB, Ez cắt SC tại F
Trong (SBD), kẻ Jt // SB, Jt cắt SD tại I
⇒ IJ // (SAB)
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. khi đó ta có.
A. MN // (SCD)
B. EF // (SAD)
C. NF // (SAD)
D. IJ // (SAB)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}\right)\)
Trước hết ta chứng minh 1 bổ đề đơn giản về diện tích tam giác như sau (em tự vẽ hình)
Cho tam giác ABC, trên các cạnh AB và AC lần lượt lấy 2 điểm B' và C', khi đó ta có:
\(\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{AB'.AC'}{AB.AC}\)
Chứng mình: từ C và C' lần lượt hạ CH và C'H' vuông góc AB, khi đó CH song song C'H' nên theo Talet:
\(\dfrac{C'H'}{CH}=\dfrac{AC'}{AC}\)
\(\Rightarrow\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{\dfrac{1}{2}C'H'.AB'}{\dfrac{1}{2}CH.AB}=\dfrac{AC'.AB'}{AC.AB}\)
Quay lại bài, gọi O là tâm đáy
Trong mp (SAC), tại O' là giao điểm của SO và A'C'
Ba mặt phẳng (SAC), (SBD), \(\left(\alpha\right)\) cắt nhau theo 3 giao tuyến phân biệt là SO, A'C', B'D' nên 3 giao tuyến này song song hoặc đồng quy.
Mà SO và A'C' cắt nhau tại O' nên 3 đường thẳng nói trên đồng quy tại O'
Ta có:
\(S_{SA'C'}=S_{SA'O'}+S_{SC'O'}\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{S_{SAC}}+\dfrac{S_{SC'O'}}{S_{SAC}}\)
\(\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{2S_{SAO}}+\dfrac{S_{SC'O'}}{S_{SCO}}\Rightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SA'.SO'}{2SA.SO}+\dfrac{SC'.SO'}{2SC.SO}\)
\(\Leftrightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SO'}{2SO}\left(\dfrac{SA'}{SA}+\dfrac{SC'}{SC}\right)\)
\(\Leftrightarrow SA'.SC'=\dfrac{SO'}{2SO}\left(SC.SA'+SA.SC'\right)\)
\(\Leftrightarrow1=\dfrac{SO'}{2SO}\left(\dfrac{SC}{SC'}+\dfrac{SA}{SA'}\right)\)
\(\Leftrightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}=\dfrac{2SO}{SO'}\)
Hoàn toàn tương tự, ta cũng có \(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}=\dfrac{2SO}{SO'}\)
\(\Rightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}\right)=0\)
giúp tớ với tớ cần gấp ạ
Cho hình chóp S.ABCD. Tứ giác có đáy AB và CD cắt nhau tại E,AC và BD cắt nhau tại F, AC và BD cắt nhau tại G. Mặt phẳng (P) cắt SA,SB,SC lần lượt tại A’,B’,C’.
a. Tìm giao điểm D’ của SD với (P)
b. Tìm điều kiện của (P) để A'B' // C'D'
c. Tính diện tích tứ giác A'B'C'D'
Phần I: Trắc nghiệm
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
- Đặt S A → = a → , S B → = b → , S C → = c → , S D → = d → .Khẳng định nào sau đây đúng?
A. a → + c → = d → + b →
B. a → + b → = d → + c →
C. a → + d → = b → + c →
D. a → + b → + c → + d → = 0 →
Chọn A.
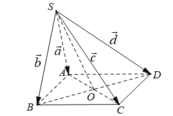
- Gọi O là tâm của hình bình hành ABCD. Ta có:
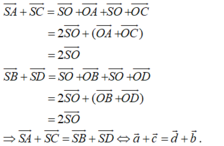
cho hình chóp S.ABCD đáy ABCD là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây
a) AB và CD
b) SA và SC
c) SB và SD
d) SA và BC
e) SD và AB
a: ABCD là hình bình hành
=>AB//CD
b: SA cắt SC tại S
=>SA và SC là hai đường thẳng cắt nhau
c: SB cắt SD tại S
=>SB và SD là hai đường thẳng cắt nhau
d: \(SA\subset\left(SAB\right)\)
\(BC\subset\left(SBC\right)\)
Do đó: SA và BC là hai đường thẳng chéo nhau
d: \(SD\subset\left(SCD\right)\)
\(AB\subset\left(ABCD\right)\)
Do đó: SD và AB là hai đường thẳng chéo nhau
cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SA=SB=SC=SD=4a
a) tính góc giữa đường thẳng SD và BC
b) tính diện tích hình chiếu vuông góc của tam giác SCD trên mặt phẳng (ABCD)
a.
Do AD song song BC nên góc giữa SD và BC là góc giữa SD và AD, cùng là góc \(\widehat{SDA}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{SDA}=\dfrac{SD^2+AD^2-SA^2}{2SD.AD}=\dfrac{1}{8}\)
\(\Rightarrow\widehat{SDA}=82^049'\)
b.
Do chóp có các cạnh bên bằng nhau và đáy là hình vuông nên chóp là chóp đều
Gọi O là tâm đáy \(\Rightarrow AC\perp BD\) tại O và \(SO\perp\left(ABCD\right)\)
\(\Rightarrow\Delta OCD\) là hình chiếu vuông góc của tam giác SCD lên (ABCD)
\(OC=OD=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{2AB^2}=a\sqrt{2}\)
\(\Rightarrow S_{OCD}=\dfrac{1}{2}OC.OD=a^2\)