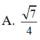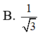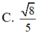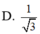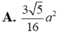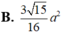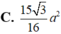Question

cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SA=SB=SC=SD=4a

a) tính góc giữa đường thẳng SD và BC

b) tính diện tích hình chiếu vuông góc của tam giác SCD trên mặt phẳng (ABCD)

Answer 1

a.

Do AD song song BC nên góc giữa SD và BC là góc giữa SD và AD, cùng là góc \(\widehat{SDA}\)

Áp dụng định lý hàm cosin:

\(cos\widehat{SDA}=\dfrac{SD^2+AD^2-SA^2}{2SD.AD}=\dfrac{1}{8}\)

\(\Rightarrow\widehat{SDA}=82^049'\)

b.

Do chóp có các cạnh bên bằng nhau và đáy là hình vuông nên chóp là chóp đều

Gọi O là tâm đáy \(\Rightarrow AC\perp BD\) tại O và \(SO\perp\left(ABCD\right)\)

\(\Rightarrow\Delta OCD\) là hình chiếu vuông góc của tam giác SCD lên (ABCD)

\(OC=OD=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{2AB^2}=a\sqrt{2}\)

\(\Rightarrow S_{OCD}=\dfrac{1}{2}OC.OD=a^2\)