Question

cho hình chóp S.ABCD có đáy là hình vuông cạnh \(a\sqrt{2}\), SA=SB=SC=SD=2a

a) tính góc giữa đường thẳng SC và AB

b) tính diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD)

Answer 1

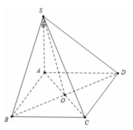
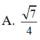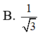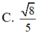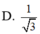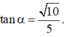a.

Do AB song song DC nên góc giữa SC và AB là góc giữa SC và CD, cùng là góc SCD

Áp dụng định lý hàm cosin:

\(cos\widehat{SCD}=\dfrac{SC^2+CD^2-SD^2}{2SC.CD}=\dfrac{1}{4}\)

\(\Rightarrow\widehat{SCD}\approx75^031'\)

b.

Gọi O là tâm đáy, do chóp có đáy là hình vuông và các cạnh bên bằng nhau nên chóp là chóp đều

\(\Rightarrow SO\perp\left(ABCD\right)\)

\(\Rightarrow\Delta OAB\) là hình chiếu vuông góc của SAB lên (ABCD)

\(OA=OB=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AB^2+BC^2}=a\)

Mặt khác OA vuông góc OB (2 đường chéo hình vuông)

\(\Rightarrow S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{a^2}{2}\)