Question

Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a và SA=SB=SC=SD=a^2 gọi O là giao điểm của AC và BD Tính góc giữa đường thẳng SC và mặt phẳng ABCD

Answer 1

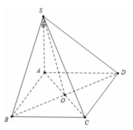
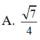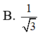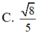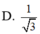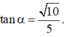Sửa đề; SA=SB=SC=SD=2a

SA=SB

OA=OB

=>SO là trung trực của AB

=>SO vuông góc AB(2)

SA=SD

OA=OD

=>SO là trung trực của AD
=>SO vuông góc AD(1)

Từ (1), (2) suy ra SO vuông góc (ABCD)

(SC;(ABCD))=(CS;CO)=góc SCO

\(OC=\dfrac{a\sqrt{2}}{2}\)

\(SO=\sqrt{SA^2+AO^2}\)

\(=\sqrt{\left(2a\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\sqrt{4a^2+\dfrac{1}{2}a^2}=\dfrac{3}{\sqrt{2}}a\)

\(SC=\sqrt{SO^2+OC^2}=\sqrt{\dfrac{9}{2}a^2+\dfrac{1}{2}a^2}=a\sqrt{5}\)

\(cosSCO=\dfrac{OC}{SC}\)

\(=\dfrac{a\sqrt{2}}{2}:a\sqrt{5}=\dfrac{\sqrt{2}}{2\sqrt{5}}\)

=>\(\widehat{SCO}\simeq72^0\)

=>\(\left(SC;\left(ABCD\right)\right)=72^0\)