A là đáp án đúng (do BC song song AD, mà SA, SD, AD cùng thuộc mp (SAD)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Với giả thiết: hình chóp S.ABCD có đáy là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Ta có:
A. MN // (SCD)
B. EF //(SAD)
C. NF // (SAD)
D. IJ //(SAB)
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. khi đó ta có.
A. MN // (SCD)
B. EF // (SAD)
C. NF // (SAD)
D. IJ // (SAB)
Phần I: Trắc nghiệmCho hình chóp S.ABCD có đáy ABCD là hình bình hành. - Đặt
S
A
→
a
→
,
S
B
→
b
→
,
S
C
→
c
→
,
S
D
→
d...
Đọc tiếp
Phần I: Trắc nghiệm
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
- Đặt S A → = a → , S B → = b → , S C → = c → , S D → = d → .Khẳng định nào sau đây đúng?
A. a → + c → = d → + b →
B. a → + b → = d → + c →
C. a → + d → = b → + c →
D. a → + b → + c → + d → = 0 →
cho hình chóp S.ABCD đáy ABCD là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây
a) AB và CD
b) SA và SC
c) SB và SD
d) SA và BC
e) SD và AB
cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SA=SB=SC=SD=4a
a) tính góc giữa đường thẳng SD và BC
b) tính diện tích hình chiếu vuông góc của tam giác SCD trên mặt phẳng (ABCD)
cho hình chóp S.ABCD đáy ABCD là hình chữ nhật. Xét vị trí tương đối của các cặp đường thẳng sau đây
a) AD và BC
b) SB và SC
c) SA và SD
d) SB và CD
e) SC và AD
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB a
2
và SASBSCSD2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB = a 2 và SA=SB=SC=SD=2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
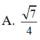
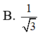
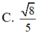
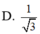
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SASC; SBSD. Trong các khẳng định sau, khẳng định nào đúng?
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA=SC; SB=SD. Trong các khẳng định sau, khẳng định nào đúng?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA SC và SB SD. Khẳng định nào sau đây sai? A.
S
O
⊥
A
B
C
D
B.
C
D
⊥
S
B
D
C.
A
B
⊥
S
A
C
D.
C...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây sai?
A. S O ⊥ A B C D
B. C D ⊥ S B D
C. A B ⊥ S A C
D. C D ⊥ A C





