\(2x^2-5x+4< 0\)

<=> \(2\left(x^2-\frac{5}{2}x+2\right)< 0\)

<=> \(x^2-\frac{5}{2}x+2< 0\)

<=> \(x^2-2\times x\times\frac{5}{4}+\frac{25}{16}-\frac{25}{16}+2< 0\)

<=> \(\left(x-\frac{5}{4}\right)^2< -0,4375\)

Điều này là vô lí vì \(\left(x-\frac{5}{4}\right)^2\ge0\)

2:

a: =>2x^2-4x-2=x^2-x-2

=>x^2-3x=0

=>x=0(loại) hoặc x=3

b: =>(x+1)(x+4)<0

=>-4<x<-1

d: =>x^2-2x-7=-x^2+6x-4

=>2x^2-8x-3=0

=>\(x=\dfrac{4\pm\sqrt{22}}{2}\)

Lời giải:

b/

\(\frac{3x+5}{2x^2-5x+3}\geq 0\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} 3x+5\geq 0\\ 2x^2-5x+3>0\end{matrix}\right.\\ \left\{\begin{matrix} 3x+5\leq 0\\ 2x^2-5x+3<0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x\geq \frac{-5}{3}\\ x>\frac{3}{2}(\text{hoặc}) x< 1\end{matrix}\right.\\ \left\{\begin{matrix} x\leq \frac{-5}{3}\\ 1< x< \frac{3}{2}\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow \left[\begin{matrix} x>\frac{3}{2}\\ \frac{-5}{3}\leq x< 1\end{matrix}\right.\ \)

c/

$2x^3+x+3>0$

$\Leftrightarrow 2x^2(x+1)-2x(x+1)+3(x+1)>0$

$\Leftrightarrow (x+1)(2x^2-2x+3)>0$

$\Leftrightarrow (x+1)[x^2+(x-1)^2+2]>0$

$\Leftrightarrow x+1>0$

$\Leftrightarrow x>-1$

\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)

\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)

Bảng xét dấu:

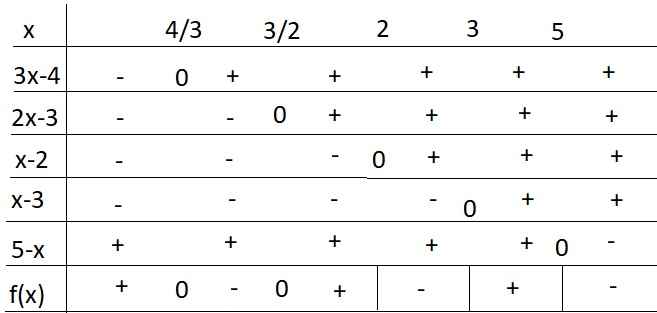
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)

x-1 + x-3 =1 <=> 2x -4=1 tu giai not

a)      \(2{x^2} - 3x + 1 > 0\)

Tam thức \(f\left( x \right) = 2{x^2} - 3x + 1\) có \(a + b + c = 2 - 3 + 1 = 0\) nên hai nghiệm phân biệt \({x_1} = 1\) và \({x_2} = \frac{1}{2}.\)

Mặt khác \(a = 2 > 0,\) do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là: \(S= \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {1; + \infty } \right).\)

b)     \({x^2} + 5x + 4 < 0\)

Tam thức \(f\left( x \right) = {x^2} + 5x + 4\) có \(a - b + c = 1 - 5 + 4 = 0\) nên phương trình có hai nghiệm phân biệt \(x =  - 1\) và \(x =  - 4.\)

Mặt khác \(a = 1 > 0,\) do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là: \(S = \left( { - 4; - 1} \right).\)

c)      \( - 3{x^2} + 12x - 12 \ge 0\)

Tam thức \(f\left( x \right) =  - 3{x^2} + 12x - 12 =  - 3\left( {{x^2} - 4x + 4} \right) =  - 3{\left( {x - 2} \right)^2} \le 0\)

Do đó 

\( - 3{x^2} + 12x - 12 \ge 0 \Leftrightarrow  - 3{x^2} + 12x - 12 = 0 \Leftrightarrow  - 3{\left( {x - 2} \right)^2} = 0 \Leftrightarrow x = 2.\)

Tập nghiệm của bất phương trình là: \(S = \left( { 2} \right).\)

d)     \(2{x^2} + 2x + 1 < 0.\)

Tam thức \(f\left( x \right) = 2{x^2} + 2x + 1\) có \(\Delta  =  - 1 < 0,\) hệ số \(a = 2 > 0\) nên \(f\left( x \right)\) luôn dướng với mọi \(x,\) tức là \(2{x^2} + 2x + 1 > 0\) với mọi \(x \in \mathbb{R}.\)

\( \Rightarrow \) bất phương trình vô nghiệm

a) Ta có \(a = 2 > 0\) và \(\Delta  = {\left( { - 5} \right)^2} - 4.2.3 = 1 > 0\)

=> \(2{x^2} - 5x + 3 = 0\) có 2 nghiệm phân biệt \({x_1} = 1,{x_2} = \frac{3}{2}\).

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} - 5x + 3\) mang dấu “+” là \(\left( { - \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)

Vậy tập nghiệm của bất phương trình \(2{x^2} - 5x + 3 > 0\) là \(\left( { - \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)

b) Ta có \(a =  - 1 < 0\) và \(\Delta ' = {\left( { - 1} \right)^2} - \left( { - 1} \right).8 = 9 > 0\)

=> \( - {x^2} - 2x + 8 = 0\)có 2 nghiệm phân biệt \({x_1} =  - 4,{x_2} = 2\).

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - {x^2} - 2x + 8\) mang dấu “-” là \(\left( { - \infty ; - 4} \right] \cup \left[ {2; + \infty } \right)\)

Vậy tập nghiệm của bất phương trình \( - {x^2} - 2x + 8 \le 0\) là \(\left( { - \infty ; - 4} \right] \cup \left[ {2; + \infty } \right)\)

c)

Ta có \(a = 4 > 0\) và \(\Delta ' = {\left( { - 6} \right)^2} - 4.9 = 0\)

=> \(4{x^2} - 12x + 9 = 0\) có nghiệm duy nhất \(x = \frac{3}{2}\).

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(4{x^2} - 12x + 9\) mang dấu “-” là \(\emptyset \)

Vậy tập nghiệm của bất phương trình \(4{x^2} - 12x + 9 < 0\) là \(\emptyset \)

d) \( - 3{x^2} + 7x - 4 \ge 0\)

Ta có \(a =  - 3 < 0\) và \(\Delta  = {7^2} - 4.\left( { - 3} \right).\left( { - 4} \right) = 1 > 0\)

=> \( - 3{x^2} + 7x - 4 = 0\) có 2 nghiệm phân biệt \({x_1} = 1;{x_2} = \frac{4}{3}\).

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 7x - 4\) mang dấu “+” là \(\left[ {1;\frac{4}{3}} \right]\)

Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 7x - 4 \ge 0\) là \(\left[ {1;\frac{4}{3}} \right]\)

c: =>2x+4>=2x+2-3

=>4>=-1(luôn đúng)

a: 5x+10>3x+3

=>2x>-7

=>x>-7/2

bạn coi lại đề nhé!

a: =>x+2<=0

=>x<=-2

b: =>-x>-1

=>x<1

c: =>2x+4>=2x+2-3

=>4>=-1(luôn đúng)

d: =>2x+2<5x-10-3x

=>2x+2<2x-10

=>2<-10(loại)