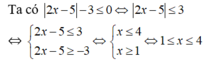Với x thuộc tập hợp nào dưới đây thì nhị thức bậc nhất f(x) = \(\left[2x-5\right]-3\) không dương

Những câu hỏi liên quan
Với x thuộc tập hợp nào dưới đây thì nhị thức bậc nhất f(x) = \(\left|2x-5\right|-3\) không dương
\(\left|2x-5\right|-3\le0\)
\(\Leftrightarrow\left|2x-5\right|\le3\)
\(\Leftrightarrow-3\le2x-5\le3\)
\(\Leftrightarrow1\le x\le4\)
Đúng 2
Bình luận (1)
Với x thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
f
(
x
)
1
|
x
|
-
3
-
1
2
luôn âm. A. x -5 hay x -3 B. x 3 hay x 5 C. |x| 3 hay |x| 5. D. luôn đúng với mọi x
Đọc tiếp
Với x thuộc tập hợp nào dưới đây thì nhị thức bậc nhất f ( x ) = 1 | x | - 3 - 1 2 luôn âm.
A. x < -5 hay x > -3
B. x < 3 hay x > 5
C. |x| < 3 hay |x| > 5.
D. luôn đúng với mọi x
Chọn C
Ta có
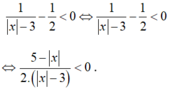
Đặt ![]() bpt trở thành
bpt trở thành 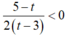
Bảng xét dấu
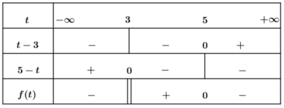
Căn cứ bảng xét dấu ta được
![]()
Đúng 0
Bình luận (0)
Với x thuộc tập hợp nào dưới đây thì biểu thức
f
(
x
)
|
2
x
-
5
|
-
3
không dương A. 1≤ x≤ 4 B. x 2,5 C. x 0 D. x 1
Đọc tiếp
Với x thuộc tập hợp nào dưới đây thì biểu thức f ( x ) = | 2 x - 5 | - 3 không dương
A. 1≤ x≤ 4
B. x = 2,5
C. x = 0
D. x < 1
Với x thuộc tập hợp nào dưới đây thì f(x)= 2x +\(\dfrac{3}{2x-4}-\left(3+\dfrac{3}{2x-4}\right)\)âm
A. 2x < 3
B. x <\(\dfrac{3}{2}\) và x ≠ 2
C. x < \(\dfrac{3}{2}\)
D. Tất cả đều đúng
\(f\left(x\right)=2x+\dfrac{3}{2x-4}-\left(3+\dfrac{3}{2x-4}\right)\)
\(f\left(x\right)=2x+\dfrac{3}{2x-4}-3-\dfrac{3}{2x-4}\)
\(f\left(x\right)=2x-3\)
Để f(x) âm thì :
\(2x-3< 0\)
\(\Leftrightarrow2x< 3\)
\(\Leftrightarrow x< \dfrac{3}{2}\)
Vậy C đúng
Have a nice day!
Đúng 1
Bình luận (0)
Với x thuộc tập hợp nào dưới đây thì f(x) = x(5x + 2) - x( x 2 + 6) không dương
A. ( - ∞ ;1] ∪ [4; + ∞ )
B. [1;4]
C. (1;4)
D. [0;1] ∪ [4; + ∞ )
Chọn D.
Để f(x) = x(5x + 2) - x( x 2 + 6) không dương thì
x(5x + 2) - x(x2 + 6) ≤ 0 ⇔ x( x 2 - 5x + 4) ≥ 0
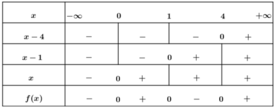
Vậy x ∈ [0;1] ∪ [4; + ∞ ).
Đúng 0
Bình luận (0)
Với x thuộc tập hợp nào thì nhị thức f(x) = x(x^2 - 1) không âm?
Xét f(x) = \(x\left(x^2-1\right)=x\left(x-1\right)\left(x+1\right)\)
f(x) = 0 khi x = 0 hoặc x = 1 hoặc x = -1
Ta có bảng
x \(-\infty\) -1 0 1 \(+\infty\)
x - | - 0 + | +
x-1 - | - | - 0 +
x+1 - 0 + | + | +
f(x) - 0 + 0 - 0 +
=> f(x) \(\ge0\Leftrightarrow x\in\left[-1;0\right]\cup\left[1;+\infty\right]\)
Đúng 0
Bình luận (0)
Cho nhị thức bậc nhất f(x) = 4-2x. Trong các khẳng định sau , khẳng định nào đúng ?
\(A,f\left(x\right)>0với\forall x\in\left(-\infty;2\right)\)
\(B,f\left(x\right)>0với\forall x\in(-\infty;-2]\)
C,\(f\left(x\right)>0với\forall x\in\left(2;+\infty\right)\)
\(D,f\left(x\right)< 0với\forall x\in\left(-\infty;2\right)\)
Với giá trị nào của x thì tam thức bậc hai \(f\left( x \right) = 2{x^2} - 5x + 3\) mang dấu dương?
Tam thức \(f\left( x \right) = 2{x^2} - 5x + 3\) có \(\Delta = 1 > 0\), hai nghiệm phân biệt là \({x_1} = 1,{x_2} = \frac{3}{2}\) và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
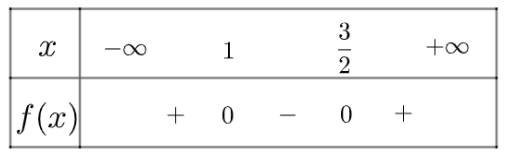
Vậy tam thức đã cho mang dấu dương khi x nằm trong khoảng \(\left( { - \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
2
x
−
3
x
2
. Để
f
(
x
)
0
thì x có giá trị thuộc tập hợp nào dưới đây? A.
−
∞
;
1
3...
Đọc tiếp
Cho hàm số f ( x ) = 2 x − 3 x 2 . Để f ' ( x ) < 0 thì x có giá trị thuộc tập hợp nào dưới đây?
A. − ∞ ; 1 3
B. 0 ; 1 3
C. 1 3 ; 2 3
D. 1 3 ; + ∞
Ta có
f ' ( x ) < 0 ⇔ 2 - 6 x 2 2 x - 3 x 2 < 0 ⇔ 2 x - 3 x 2 > 0 2 - 6 x < 0 ⇔ 0 < x < 2 3 x > 1 3 ⇒ x ∈ 1 3 ; 2 3
Chọn đáp án C
Đúng 0
Bình luận (0)