Cho tam giác ABC có B=40^0 C=30^0 . Tia phân giác của A cắt BC Ở D.Tính ADC, ADB
Cho tam giác ABC có góc B - góc C = a,tia phân giác của góc A cắt BC ở D.Tính góc ADC,góc ADB.
Lời giải:
Do $AD$ là phân giác $\widehat{A}$ nên $\widehat{DAC}=\widehat{DAB}$
Ta có:
$\widehat{ADB}=\widehat{DAC}+\widehat{C}$
$\widehat{ADC}=\widehat{DAB}+\widehat{B}$
$\Rightarrow \widehat{ADC}-\widehat{ADB}=\widehat{B}-\widehat{C}=\alpha$
Mà $\widehat{ADC}+\widehat{ADB}=180^0$
Do đó:
$\widehat{ADC}=\frac{180^0+\alpha}{2}$
$\widehat{ADB}=\frac{180^0-\alpha}{2}$
Cho tam giác ABC có góc B trừ góc C bằng 20 độ tia phân giác của góc A cắt BC ở D.Tính số đo góc ADC và góc ADB
Cho tam giác có góc B= \(70^0\), góc C= \(40^0\). Tia phân giác của góc A cắt BC ở D. Tính góc ADC,ADB
\(\widehat{BAC}=180^0-\widehat{B}-\widehat{C}=70^0\)
AD là p/g nên \(\widehat{A_1}=\widehat{A_2}=\dfrac{1}{2}\widehat{BAC}=35^0\)
Ta có \(\widehat{ADB}=180^0-\widehat{B}-\widehat{A_1}=180^0-70^0-35^0=75^0\)
\(\widehat{ADC}=180^0-\widehat{C}-\widehat{A_2}=180^0-40^0-35^0=105^0\)
Cho tam giác ABC có B - C =20 ĐỘ.Tia phân giác của góc A cắt BC ở D.Tính số đo các góc ADC VÀ ADB
cho tam giác ABC có B-C=20 độ.Tia phân giác của góc A cắt BC ở D.Tính số đo góc ADB và góc ADC
Cho tam giác ABC có \(\widehat{B}=80^0,\widehat{C}=30^0\). Tia phân giác của góc A cắt BC ở D. Tính \(\widehat{ADC},\widehat{ADB}\) ?
\(\widehat{BAC}\)= 1800 - (\(\widehat{B}+\widehat{C}\)) = 1800 - ( 800 + 300)= 700
\(\widehat{A}_1\)=\(\widehat{A}_2\)=\(\dfrac{\widehat{A}}{2}\)=\(\dfrac{70^0}{2}\)= 350
\(\widehat{ADC}=\widehat{B}+\widehat{A}_1\)(Góc ngoài của tam giác)
=800 + 350)= 1150
Do đó \(\widehat{ADB}\)= 1800 - \(\widehat{ADC}\)= 1800 + 1150=650
Hình vẽ: 

Gọi A1, A2 là 2 góc được tạo ra bởi tia phân giác góc A.
Ta có:
Góc ∠BAC = 1800 – ( ∠B + ∠C)
= 1800 – ( 800 + 300) = 700
Hay ta có thể gọi ∠A = 700
Góc ∠A1 = ∠A2
= ∠A/2 = 700 /2 = 350
Xét tam giác ADC ta có: Góc ∠ADC = 1800 – (∠C + ∠A2)= 1800 – (350 + 300)= 1150
Do đó góc ∠ADB = 1800 – ∠ADC= 1800 – 1150
= 650
Giải:
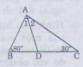
ˆBACBAC^= 1800 - (ˆBB^+ˆCC^) = 1800 - ( 800 + 300)= 700
ˆA1A1^=ˆA2A2^=ˆA2A^2=70027002= 350
ˆADCADC^=ˆBB^+ˆA1A1^(Góc ngoài của tam giác)
=800 + 350)= 1150
Do đó ˆADBADB^= 1800 - ˆADCADC^= 1800 + 1150=650
cho tam giác ABC có B=70o,C=30o
a) kẻ AH vuông góc với BC.tính các góc HAB,HAC
b)kẻ tia phân giác của góc A cắt Bc tại D.tính các góc ADC,ADB
Cho tam giác ABC có B bằng 70 độ C bằng 30 độ tia phân giác của góc A cắt BC ở D. Tính ADC=?,ADB=?
cho tam giác ABC có góc Atrừ góc B = 20 độ.Tia phân giác của góc A cắt BC ở D.Tính số đo các góc ADC,góc ADB