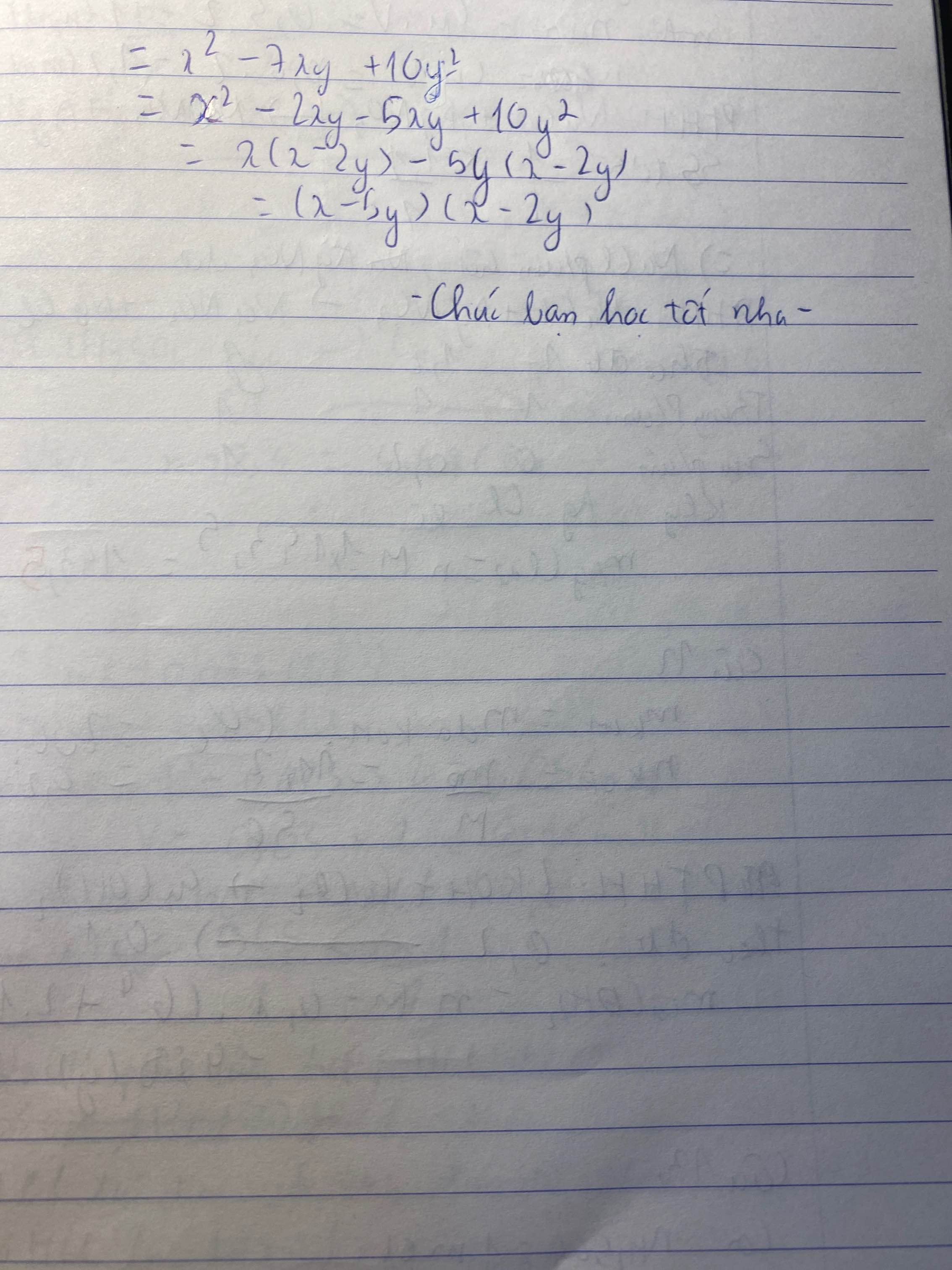\(4x^2-9y^2+4x-6y=\left(4x^2-9y^2\right)+\left(4x-6y\right)=\left(2x-3y\right)\left(2x+3y\right)+2\left(2x-3y\right)=\left(2x-3y\right)\left(2x+3y+2\right)\)

\(4x^2-9y^2+4x-6y\)

\(=\left(2x-3y\right)\left(2x+3y\right)+2\left(2x-3y\right)\)

\(=\left(2x-3y\right)\left(2x+3y+2\right)\)

=5(x²-9)

=5(x²-3²)

=5(x-3)(x+3)

\(3x^2-7x+4=\left(3x^2-3x\right)-\left(4x-4\right)=3x\left(x-1\right)-4\left(x-1\right)=\left(x-1\right)\left(3x-4\right)\)

3x^2 -7x+4

= 3x^2 -3x-4x+4

= 3x ( x-1) -4(x-1)

= (3x-4)(x-1)

3x^2 - 7x  + 4 =3x ^2 - 4x - 3x  + 4 = 3x(x-1) - 4 ( x+ 1)= (3x-4)(x-1)

\(=x^2-2xy-5xy+10y^2=x\left(x-2y\right)-5y\left(x-2y\right)=\left(x-2y\right)\left(x-5y\right)\)

Đây bạn nhé!

\(=x\left[x^2\left(x-y\right)^2-36y^2\right]\\ =x\left[x\left(x-y\right)-6y\right]\left[x\left(x-y\right)+6y\right]\\ =x\left(x^2-xy-6y\right)\left(x^2-xy+6y\right)\)

\(\left(xy+1\right)^2-\left(x+y\right)^2=\left(xy+1-x-y\right)\left(xy+1+x+y\right)=\left[x\left(y-1\right)-\left(y-1\right)\right]\left[x\left(y+1\right)+\left(y+1\right)\right]=\left(x-1\right)\left(y-1\right)\left(x+1\right)\left(y+1\right)\)

\(\left(xy+1\right)^2-\left(x+y\right)^2\)

\(=\left(xy-x-y+1\right)\left(xy+1+x+y\right)\)

\(=\left(y-1\right)\left(x-1\right)\left(y+1\right)\left(x+1\right)\)

\(\left(ab-1\right)^2+\left(a+b\right)^2=a^2b^2-2ab+1+a^2+2ab+b^2=a^2+b^2+a^2b^2+1=a^2\left(b^2+1\right)+\left(b^2+1\right)=\left(a^2+1\right)\left(b^2+1\right)\)

\(\left(ab-1\right)^2+\left(a+b\right)^2=a^2b^2-2ab+1+a^2+2ab+b^2=a^2b^2+a^2+b^2+1=\left(a^2b^2+a^2\right)+\left(b^2+1\right)=a^2\left(b^2+1\right)+\left(b^2+1\right)=\left(a^2+1\right)\left(b^2+1\right)\)

\(\left(ab-1\right)^2+\left(a+b\right)^2\)

\(=a^2b^2+1+a^2+b^2\)

\(=\left(a^2+1\right)\left(b^2+1\right)\)

\(9x^2+6x-4y^2+4y=\left(9x^2+6x+1\right)-\left(4y^2-4y+1\right)=\left(3x+1\right)^2-\left(2y-1\right)^2=\left(3x+1-2y+1\right)\left(3x+1+2y-1\right)\)

\(9x^2+6x-4y^2+4y=\left(9x^2+6x+1\right)-\left(4y^2-4y+1\right)=\left(3x+1\right)^2-\left(2x-1\right)^2=\left(3x+1-2y+1\right)\left(3x+1+2y-1\right)=\left(3x-2x+2\right)\left(3x+2y\right)\)

\(9x^2+6x-4y^2+4y\)

\(=\left(3x+2y\right)\left(3x-2y\right)+2\left(3x+2y\right)\)

\(=\left(3x+2y\right)\left(3x-2y+2\right)\)

`(ax+by)^2-(ay+bx)^2`

`=(ax+by+ay+bx)(ax+by-ay-bx)`

`=[a(x+y)+b(x+y)][a(x-y)-b(x-y)]`

`=(x+y)(a+b)(x-y)(a-b)`

\(\left(ax+by\right)^2-\left(ay+bx\right)^2\)

\(=\left(ax-ay-bx+by\right)\left(ax+ay+bx+by\right)\)

\(=\left(x-y\right)\left(a-b\right)\left(x+y\right)\left(a+b\right)\)