cho tam giác ABC nhọn
chứng minh rằng : AB2=AC2 +BC2-2.AC.BC.cosC
Cho tam giác ABC có ∠A = 60 0 Chứng minh rằng:
B C 2 = A B 2 + A C 2 - AB.AC
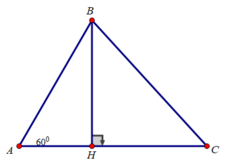
Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) = 60 0
BH = AB.sin A = AB.sin 60 0 = (AB 3 )/2
AH = AB.cos A = AB.cos 60 0 = AB/2
Xét tam giác BHC vuông tại H có:
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2
= B H 2 + A C 2 - 2 A C . A H + A H 2
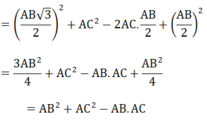
Vậy được điều phải chứng minh.
Cho tam giác ABC có ∠ A = 60 ° . Chứng minh rằng: B C 2 = A B 2 + A C 2 - A B . A C
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠ (BAC) = 60 ° là góc nhọn), do đó H C 2 = A C - A H 2 (xem h.bs.8a, 8b)
Công thức Py-ta-go cho ta
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2 = B H 2 + A C 2 + A H 2 - 2 A C . A H = A B 2 + A C 2 - 2 A C . A H
Do ∠ (BAC) = 60 ° nên AH = AB.cos 60 ° = AB/2, suy ra B C 2 = A B 2 + A C 2 - A B . A C
Câu 20: Tam giác ABC vuông tại B suy ra:
A. AC2 = AB2 + BC2 B. AC2 = AB2 - BC2
C. BC2 = AB2 + AC2 D. AB2 = BC2 + AC2
Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C
C. Tại A D. Không phải là tam giác vuông
Câu 22: Cho ABC có = 900 ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:
A. 6,5 cm B. 5,5 cm C. 6 cm D. 6,2 cm
Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:
A. 3cm, 4dm, 5cm. B. 5cm, 14cm, 12cm.
C. 5cm, 5cm, 8cm. D. 9cm, 15cm, 12cm.
Câu 24: Cho ABC có AB = AC và = 600, khi đó tam giác ABC là:
A. Tam giác vuông B. Tam giác cân
C. Tam giác đều D. Tam giác vuông cân
Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:
A. ∠A ≤ 900 B. ∠A > 900 C. ∠A < 900 D. ∠A = 900
Ai giúp mình với ạ!
Câu 20: Tam giác ABC vuông tại B suy ra:
A. AC2 = AB2 + BC2 B. AC2 = AB2 - BC2
C. BC2 = AB2 + AC2 D. AB2 = BC2 + AC2
Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C
C. Tại A D. Không phải là tam giác vuông
Câu 22: Cho ABC có = 900 ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:
A. 6,5 cm B. 5,5 cm C. 6 cm D. 6,2 cm
Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:
A. 3cm, 4dm, 5cm. B. 5cm, 14cm, 12cm.
C. 5cm, 5cm, 8cm. D. 9cm, 15cm, 12cm.
Câu 24: Cho ABC có AB = AC và = 600, khi đó tam giác ABC là:
A. Tam giác vuông B. Tam giác cân
C. Tam giác đều D. Tam giác vuông cân
Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:
A. ∠A ≤ 900 B. ∠A > 900 C. ∠A < 900 D. ∠A = 900
Cho tam giác ABC, đường cao AH. Chứng minh: AB2+AC2=BC2
Cho tam giác cân ABC (AB = AC), đường cao CD (D ở giữa A và B).
Chứng minh rằng: AB2 + BC2 + AC2 = BD2 + 2AD2 + 3DC2
Cho tam giác ABC trực tâm H nội tiếp đường tròn (O ; R). Chứng minh rằng
AH2 + BC2 = BH2 + AC2 = CH2 + AB2 = 4R2
cho tam giác ABC . M là trung điểm BC . c m AB2 AC2 2 AM2 BC2 2
Cho tam giác ABC có AB=5, BC=7,AC=8
a) Từ đẳng thức \(\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}\) ,Chứng minh công thức \(2\overrightarrow{AB}.\overrightarrow{AC}=\) AB2+AC2-BC2
Tính \(\overrightarrow{AB}.\overrightarrow{AC}\) , rồi suay ra giá trị của góc A
b) Tính \(\overrightarrow{CA}.\overrightarrow{CB}\)
a, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{BC}^2\)
\(\Leftrightarrow AC^2+AB^2-2\overrightarrow{AB}.\overrightarrow{AC}=BC^2\)
\(\Leftrightarrow2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}=\dfrac{5^2+8^2-7^2}{2}=20\)
b, \(2\overrightarrow{CA}.\overrightarrow{CB}=CA^2+CB^2-BC^2=CA^2\)
\(\Rightarrow\overrightarrow{CA}.\overrightarrow{CB}=\dfrac{CA^2}{2}=\dfrac{8^2}{2}=32\)
Lời giải:
a)
\(\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}\)
\(\Rightarrow (\overrightarrow{AC}-\overrightarrow{AB})^2=\overrightarrow{BC}^2\Leftrightarrow AB^2+AC^2-2\overrightarrow{AC}.\overrightarrow{AB}=BC^2\)
\(\Leftrightarrow 2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\) (đpcm)
Ta có:
\(\overrightarrow{AB}.\overrightarrow{AC}=\frac{AB^2+AC^2-BC^2}{2}=\frac{5^2+8^2-7^2}{2}=20\)
\(\cos \angle A=\frac{\overrightarrow{AB}.\overrightarrow{AC}}{|\overrightarrow{AB}|.|\overrightarrow{AC}|}=\frac{20}{5.8}=\frac{1}{2}\)
\(\Rightarrow \angle A=60^0\)
b)
Tương tự phần a, \(\overrightarrow{CA}.\overrightarrow{CB}=\frac{CA^2+CB^2-AB^2}{2}=\frac{8^2+7^2-5^2}{2}=44\)
Tam giác ABC vuông tại C khi đó ta có
A. AB2= AC2 + BC2 B. CB2= AC2 + BA2
C. AB= AC+ BC D. CB= AC + BA
Cho tam giác ABC có ba góc nhọn và AH là đường cao
a, Chứng minh: A B 2 + C H 2 = A C 2 + B H 2
b, Vẽ trung tuyến AM của tam giác ABC, chứng minh:
1. A B 2 + A C 2 = B C 2 2 + 2 A M 2
2. A C 2 - A B 2 = 2 B C . H M (với AC > AB)
a, Sử dụng định lí Pytago cho các tam giác vuông HAB và HAC để có đpcm
b, 1. Chứng minh tương tự câu a)
2. Sử dụng định lí Pytago cho tam giác vuông AHM