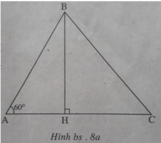
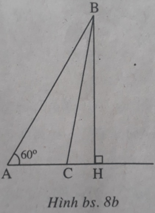
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠ (BAC) = 60 ° là góc nhọn), do đó H C 2 = A C - A H 2 (xem h.bs.8a, 8b)
Công thức Py-ta-go cho ta
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2 = B H 2 + A C 2 + A H 2 - 2 A C . A H = A B 2 + A C 2 - 2 A C . A H
Do ∠ (BAC) = 60 ° nên AH = AB.cos 60 ° = AB/2, suy ra B C 2 = A B 2 + A C 2 - A B . A C
Cho tam giác ABC có BC = a, AC = b, AB = c. Chứng minh rằng :
a) Nếu góc A = 30 độ thì a^2 = b^2 + c^2 - bc\(\sqrt{3}\)
b) Nếu góc A = 60 độ thì a^2 = b^2 + c^2 - bc
Cho tam giác ABC có số đo 3 cạnh là a,b,c.
Chứng minh rằng:
a)Nếu tam giác ABC có góc A bằng 60 độ thì S(ABC)=\(\frac{\sqrt{3}}{4}\cdot\left[a^2-\left(b-c\right)^2\right]\)
b)Nếu góc A bằng 120 độ thì sao?
Cho tam giác ABC có góc A = 120o, BC = a , AC= b, AB= c. Chứng minh rằng a^2 = b^2 +c^2+bc
Cho tam giác ABC nhọn có AB = c , AC = b , BC =a . Chứng minh rằng : \(a^2=b^2+c^2-2bc.\cos A\)
Cho tam giác ABC có a,b,c là độ dài 3 cạnh của tam giác, trong đó a lớn nhất. Chứng minh rằng tam giác ABC vuông khi và chỉ khi \(\left(\sqrt{a+b}+\sqrt{a-b}\right)\left(\sqrt{a+c}+\sqrt{a-c}\right)=\left(a+b+c\right)\sqrt{2}\)
cho tam giác ABC có góc A = 120 , BC=a , AC= b , AB =c,
chứng minh rằng
a2 = b2+c2+bc
Cho tam giác ABC có độ dài ba cạnh là a,b,c và có chu vi là 2. Chứng minh rằng \(a^2+b^2+c^2+2abc< 2\)
Chứng minh rằng: trong mọi tam giác ABC ta đều có:
a^3.(b^2 - c^2) + b^3.(c^2 - a^2) + c^3.(a^2 - b^2) \(\le\)0
Cho tam giác ABC có góc A=120 độ, BC =a, AC =b, AB =c.
Chứng minh rằng \(a^2=b^2+c^2+bc\)
Cho tam giác ABC nhọn, BC=a, AC=b, AB=c. Chứng minh rằng: b2=a2+c2-2ac.cosB.
