Trong mặt phẳng Oxy, cho hai điểm A(3;1), B(-3;4)
a.Viết phương trình đường tròn (C) có tâm A và đi qua điểm B.
b.Viết phương trình đường (C) có đường kính AB.
a) Tính khoảng cách từ gốc toạ độ C(0;0) đến điểm M(3 ; 4) trong mặt phẳng toạ độ Oxy.
b) Cho hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy. Nêu công thức tính độ dài đoạn thẳng IM.
a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)
trong mặt phẳng Oxy cho hai điểm A(-1;5) và B(3;-1) trung điểm I của đoạn thẳng AB có độ là
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1+3}{2}=1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{5+\left(-1\right)}{2}=2\end{matrix}\right.\)
\(\Rightarrow I\left(1;2\right)\)
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 3) và B(4; 2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B
A. C − 5 3 ; 0 .
B. C 5 3 ; 0 .
C. C − 3 5 ; 0 .
D. C 3 5 ; 0 .
Ta có C ∈ O x nên C(x, 0) và A C → = x − 1 ; − 3 B C → = x − 4 ; − 2 .
Do C A = C B ⇔ C A 2 = C B 2 .
⇔ x − 1 2 + − 3 2 = x − 4 2 + − 2 2 ⇔ x 2 − 2 x + 1 + 9 = x 2 − 8 x + 16 + 4 ⇔ 6 x = 10 ⇔ x = 5 3 ⇒ C 5 3 ; 0
Chọn B.
1. Trong mặt phẳng Oxy, cho đường tròn (C): \(x^2+y^2-2x+4y-4=0\)và điểm M(-1;-3). Gọi I là tâm của (C). Viết phương trình đường thẳng đi qua M và cắt (C) tại hai điểm A,B sao cho tam giác IAB có diện tích lớn nhất
2. Trong mặt phẳng Oxy, cho đường tròn (C): \(x^2+y^2+4x+4y-17=0\) và điểm A(6;17). Viết phương trình tiếp tuyến của (C) biế tiếp tuyến đi qua điểm A.
Trong mặt phẳng toạ độ Oxy cho hai điểm A B (3; 1), (2; 10). Tích vô hướng OA.OB bằng bao nhiêu
\(\overrightarrow{OA}=\left(3;1\right);\overrightarrow{OB}=\left(2;10\right)\)
\(\overrightarrow{OA}\cdot\overrightarrow{OB}=3\cdot2+1\cdot10=16\)
Trong không gian Oxyz, cho hai điểm A (1; 2; 1), B (2; 1; -3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 - 2 M B 2 lớn nhất.
A . M 3 2 ; 1 2 ; 0
B . M 1 2 ; - 3 2 ; 0
C. M (0; 0; 5)
D. M (3; -4; 0)
Trong mặt phẳng Oxy, cho hai điểm F1(-4; 0) và F2(4;0) và điểm A(0; 3). Điểm M thuộc E nào sau đây thỏa MF1= 3MF2.
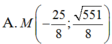
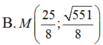
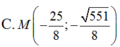
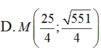
Đáp án B
- Giả sử:
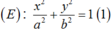
Theo giả thiết thì : c = 4 nên a2- b2= 16 (2)
(E) qua A suy ra :
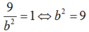
thay vào (2) ta có:
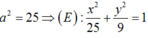
M thuộc (E)
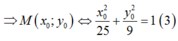
Theo tính chất của (E) ta có bán kính qua tiêu
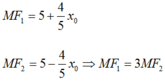
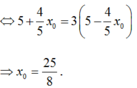
Thay vào ta có:
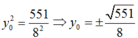
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa độ vecto u = 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4,7). Tọa độ trung điểm I của đoạn thẳng MN là
6. Cho vecto x=(-4,7) và hai vecto a=(2,-1), b=(-3,4). Nếu vecto x = m vecto a + n vecto b thì m, n là cặp số nào
Trong mặt phẳng tọa độ Oxy cho hai điểm A( 1; -1) và B(3; 2).Tìm M thuộc trục tung sao cho M A 2 + M B 2 nhỏ nhất.
A. M(0; 1)
B. M (0; -1)
C. M 0 ; 1 2 .
D. M 0 ; - 1 2 .
Ta có M ∈ O y nên M(0; m) và M A → = 1 ; − 1 − m M B → = 3 ; 2 − m .
Khi đó M A 2 + M B 2 = M A → 2 + M B → 2 = 1 2 + − 1 − m 2 + 3 2 + 2 − m 2 = 2 m 2 − 2 m + 15.
= 2 m − 1 2 2 + 29 2 ≥ 29 2 ; ∀ m ∈ ℝ .
Suy ra M A 2 + M B 2 min = 29 2 .
Dấu = xảy ra khi và chỉ khi m = 1 2 ⇒ M 0 ; 1 2 .
Chọn C.
Trong mặt phẳng tọa độ Oxy cho hai điểm A(3,-5),B(1,7). Trung điểm I của đoạn thẳng AB có tọa độ là
Áp dụng công thức tọa độ trung điểm:
\(\left\{{}\begin{matrix}x_I=\frac{x_A+x_B}{2}=2\\y_I=\frac{y_A+y_B}{2}=1\end{matrix}\right.\)
\(\Rightarrow I\left(2;1\right)\)