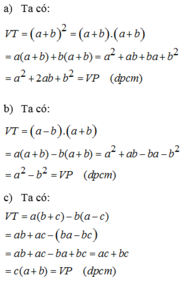cmr với mọi a,b,c,d có a2+b2>= 2ab

Những câu hỏi liên quan
a/. a4 + b4 ≥ 2a2b2
b/. (a2 + b2)2 ≥ 2a3b + 2ab3
c/. a2 - b2 ≥ 2ab (a - b)
d/. (a + b)2 ≥ 4ab
Mọi người giupps em với ạ :((
a: \(a^4+b^4\ge2a^2b^2\)
\(\Leftrightarrow a^4-2a^2b^2+b^4>=0\)
hay \(\left(a^2-b^2\right)^2\ge0\)(luôn đúng)
d: \(\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow a^2+2ab+b^2-4ab\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)(luôn đúng)
Đúng 2
Bình luận (0)
CMR :
a2 + b2 + c2 < 2( ab + bc + ca)
với mọi số thực a,b,c
Đề bài sai, phản ví dụ: \(a=b=0,c=1\)
BĐT này chỉ đúng khi a;b;c là độ dài 3 cạnh của 1 tam giác
Đúng 0
Bình luận (1)
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?A. (A – B)2 A2 – 2AB + B2 B. (A + B)2 A2 + 2AB + B2C. A2 – B2 (A + B)(A – B) D. A3 – B3 (A – B)(A2 + AB + B2)
Đọc tiếp
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?
A. (A – B)2 = A2 – 2AB + B2
B. (A + B)2 = A2 + 2AB + B2
C. A2 – B2 = (A + B)(A – B)
D. A3 – B3 = (A – B)(A2 + AB + B2)
Biến đổi vế trái thành vế phải:a)
a
+
b
2
a
2
+
2
a
b
+
b
2
b)
(
a
−
b
)
(
a
+
b
)
a
2
−
b
2
c...
Đọc tiếp
Biến đổi vế trái thành vế phải:
a) a + b 2 = a 2 + 2 a b + b 2
b) ( a − b ) ( a + b ) = a 2 − b 2
c) a ( b + c ) − b ( a − c ) = ( a + b ) c
a, a(b+c)−b(a−c)a(b+c)−b(a−c)
=ab+ac−(ab−bc)=ab+ac−(ab−bc)
=ab+ac−ab+bc=ab+ac−ab+bc
=ac+bc=ac+bc
=(a+b)c=(a+b)c
b,(a+b)(a−b)(a+b)(a−b)
=(aa+ab)−(ab+bb)=(aa+ab)−(ab+bb)
=aa+ab−ab−bb
Với a, b là hai số bất kì, trong các đẳng thức sau, đẳng thức nào không phải hằng đẳng
thức?
A. (a+b)2 =a2 +2ab+b2 B. a2 – 1 =3a C. a(2a+b) =2a2 + ab D. a(b+c) =ab+ac
Rút gọn biểu thức
a. 2x+2y/a2+2ab+b2 . ax-ay+bx-by/2x2-2y2
b. a+b-c/a2+2ab+b2-c2 . a2+2ab+b2+ac+bc/a2-b2
c.x3+1/x2+2x+1 . x2-1/2x2-2x+2
d. x8-1/x+1 . 1/ (x2+1) (x4+1)
e. x-y/xy+y2 - 3x+y/x2-xy . y-x/x+y
a2 c2... là em viết số mũ đó ạ. anh chị giúp em giải mấy bài này nha
\(=\dfrac{2\left(x+y\right)}{\left(a+b\right)^2}.\dfrac{a\left(x-y\right)+b\left(x-y\right)}{2\left(x^2-y^2\right)}\)
\(=\dfrac{2\left(x+y\right)}{\left(a+b\right)^2}.\dfrac{\left(x-y\right)\left(a+b\right)}{2\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{1}{a+b}\)
\(b,\dfrac{a+b-c}{a^2+2ab+b^2-c^2}.\dfrac{a^2+2ab+b^2+ac+bc}{a^2-b^2}\)
\(=\dfrac{a+b-c}{\left(a+b\right)^2-c^2}.\dfrac{\left(a+b\right)^2+c\left(a+b\right)}{\left(a-b\right)\left(a+b\right)}\)
\(=\dfrac{a+b-c}{\left(a+b-c\right)\left(a+b+c\right)}.\dfrac{\left(a+b\right)\left(a+b+c\right)}{\left(a-b\right)\left(a+b\right)}\)
\(=\dfrac{1}{a-b}\)
\(c,\dfrac{x^3+1}{x^2+2x+1}.\dfrac{x^2-1}{2x^2-2x+2}\)
\(=\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{\left(x+1\right)^2}.\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x^2-x+1\right)}\) \(=\dfrac{x-1}{2}\) \(d,\dfrac{x^8-1}{x+1}.\dfrac{1}{\left(x^2+1\right)\left(x^4+1\right)}\) \(=\dfrac{\left(x^4\right)^2-1}{x+1}.\dfrac{1}{\left(x^2+1\right)\left(x^4+1\right)}\) \(=\dfrac{\left(x^4-1\right)\left(x^4+1\right)}{x+1}.\dfrac{1}{\left(x^2+1\right)\left(x^4+1\right)}\) \(=\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{x+1}.\dfrac{1}{x^2+1}\) \(=\dfrac{\left(x-1\right)\left(x+1\right)}{x+1}\) \(=x-1\) \(e,\dfrac{x-y}{xy+y^2}-\dfrac{3x+y}{x^2-xy}.\dfrac{y-x}{x+y}\) \(=\dfrac{x-y}{y\left(x+y\right)}-\dfrac{3x+y}{x\left(x-y\right)}.\dfrac{-\left(x-y\right)}{x+y}\) \(=\dfrac{x-y}{y\left(x+y\right)}-\dfrac{3x+y}{x}.\dfrac{-1}{x+y}\) \(=\dfrac{x-y}{y\left(x+y\right)}-\dfrac{-3x-y}{x\left(x+y\right)}\) \(=\dfrac{x\left(x-y\right)+y\left(3x+y\right)}{xy\left(x+y\right)}\) \(=\dfrac{x^2-xy+3xy+y^2}{xy\left(x+y\right)}\) \(=\dfrac{x^2+2xy+y^2}{xy\left(x+y\right)}\) \(=\dfrac{\left(x+y\right)^2}{xy\left(x+y\right)}=\dfrac{x+y}{xy}\)
Đúng 0
Bình luận (1)
Dùng diện tích để chứng tỏ :
a
-
b
2
a
2
-
2
a
b
+
b
2
với điều kiện b a
Đọc tiếp
Dùng diện tích để chứng tỏ : a - b 2 = a 2 - 2 a b + b 2 với điều kiện b < a
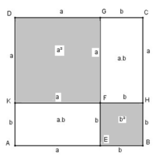
Dựng hình vuông ABCD có cạnh bằng a
Trên cạnh AB lấy điểm E sao cho BE = b
Từ E dựng đường thẳng song song BC cắt CD tại G
Ta có: CG = b, CE = ( a – b ), GD = ( a – b )
Trên cạnh AD lấy điểm K sao cho AK = b
Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F
Ta có: KD = ( a – b ), BH = b
Hình vuông ABCD có diện tích bằng a 2
Hình vuông DKFG có diện tích bằng a - b 2
Hình chữ nhật AEFK có diện tích bằng ( a – b ) b
Hình vuông EBHF có diện tích bằng b 2
Hình chữ nhật HCGF có diện tích bằng ( a – b ).b
S A B C D = S D K F G + S A E F K = S E B H F + S H C G F
nên a - b 2 + a - b b + a - b b + b 2 = a 2
⇒ a - b 2 = a 2 - 2 a b + b 2
Đúng 0
Bình luận (0)
Địa chỉ ô được viết như sau?
A. A2+B2 B. 2A + 2B C. 2,A + 2,B D. 2AB + 2 BA
Xem thêm câu trả lời
Các bạn oi giúp mình tí, cmr:
(A+b+c)^2= a2+b2+c2+2ab+2bc+2ac
(A+b+c)^2+a^2+b^2+c^2=(a+b)^2+(b+c)^2+(c+a)^2
VT = (a+b+c)^2
= [(a+b) + c]^2
= (a+b)^2 + 2(a+b)c + c^2
= a^2 + 2ab + b^2 + 2ac + 2bc + c^2
= a^2 + b^2 + c^2 + 2ab + 2ac + 2bc = VP
Vậy ...
---------------------------------------
VT= (a+b+c)^2 + a^2 + b^2 + c^2
= [(a+b) + c]^2 + a^2 + b^2 + c^2
= (a+b)^2 + 2(a+b)c + c^2 + a^2 + b^2 + c^2
= a^2 + 2ab + b^2 + 2ac + 2bc + c^2 + a^2 + b^2 + c^2
= (a^2 + 2ab + b^2) + (b^2 + 2bc + c^2) + (c^2 + 2ca + a^2)
= (a+b)^2 + (b+c)^2 + (c+a)^2 = VP
Vậy...
Đúng 0
Bình luận (0)
( a + b + c ) 2 = a ( a + b + c ) + b ( a + b + c ) + c ( a + b + c )
= a2 + ab + ac + ab + b2 + bc + ac + bc + c2
= a2 + b2 + c2 + 2ab + 2ac + 2bc
Đúng 0
Bình luận (0)
A,Cho a/b=c/d CMR (8a+9b)/(8c+9d)=(8a-9b)/(8c-9d)
B,B2=a*c CMR (A2+b2)/ (b2+c2)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{8a}{8c}=\frac{9b}{9d}\)
áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{8a}{8c}=\frac{9b}{9d}=\frac{8a+9b}{8c+9d}=\frac{8a-9b}{8c-9d}\left(dpcm\right)\)
b) xem lại đề nha b
Đúng 0
Bình luận (0)