24.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)

25.

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\Rightarrow\widehat{SAO}\) là góc giữa SA và (ABC)

\(AO=\dfrac{2}{3}.\dfrac{1.\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}\)

\(\Rightarrow cos\widehat{SAO}=\dfrac{AO}{SA}=\dfrac{1}{2}\Rightarrow\widehat{SAO}=60^0\)

26.

\(dy=y'dx=\left(x^2\right)'dx=2xdx\)

24: Ta có: \(A=10ax-5ay+2x-y\)

\(=5a\left(2x-y\right)+\left(2x-y\right)\)

\(=\left(2x-y\right)\left(5a+1\right)\)

25: Ta có: \(A=10ax-5ay-2x+y\)

\(=5a\left(2x-y\right)-\left(2x-y\right)\)

\(=\left(2x-y\right)\left(5a-1\right)\)

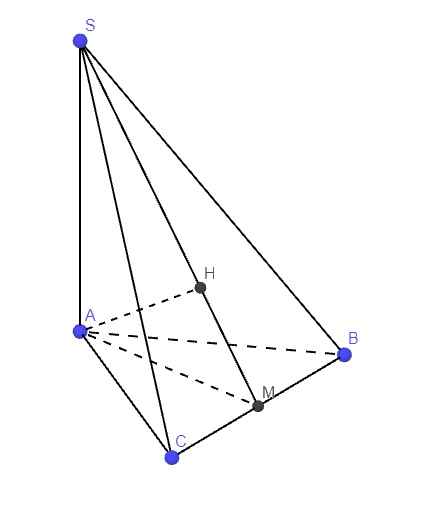
23.

Gọi M là trung điểm BC

Trong mp (SAM), từ A kẻ \(AH\perp SM\) (1)

Ta có: \(AM\perp BC\) (trung tuyến đồng thời là đường cao trong tam giác đều)

Lại có \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)

\(\Rightarrow BC\perp\left(SAM\right)\Rightarrow BC\perp SH\)

(1);(2) \(\Rightarrow SH\perp\left(SBC\right)\)

\(\Rightarrow SH=d\left(A;\left(SBC\right)\right)\)

\(AM=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)

Hệ thức lượng trong tam giác vuông SAM:

\(AH=\dfrac{AM.SA}{\sqrt{AM^2+SA^2}}=\dfrac{a\sqrt{66}}{11}\)

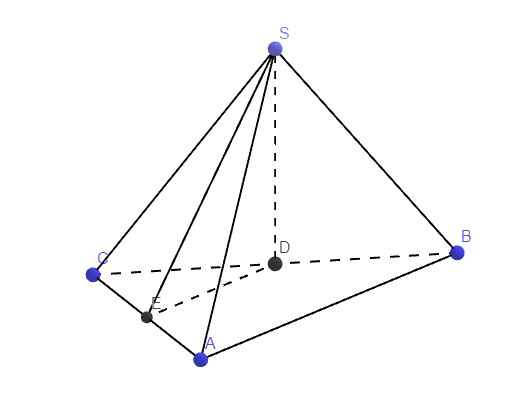
24.

Gọi D, E lần lượt là trung điểm BC, AC

\(\Rightarrow\) DE là đường trung bình tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}DE\perp AC\\DE=\dfrac{1}{2}AB\end{matrix}\right.\)

SBC đều \(\Rightarrow SD\perp BC\Rightarrow SD\perp\left(ABC\right)\)

\(\Rightarrow SD\perp AC\)

\(\Rightarrow AC\perp\left(SDE\right)\Rightarrow\widehat{SED}\) là góc giữa (SAC) và (ABC)

\(AB=BC.cos\widehat{ABC}=a.cos30^0=\dfrac{a\sqrt{3}}{2}\)

\(\Rightarrow DE=\dfrac{1}{2}AB=\dfrac{a\sqrt{3}}{4}\)

\(SD=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)

\(tan\varphi=tan\widehat{SED}=\dfrac{SD}{DE}=2\)

\(\lim\limits_{x\rightarrow+\infty}\left(ax-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}x\left(a-\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}\right)\)

Nếu \(a\ne1\Rightarrow\lim\limits_{x\rightarrow+\infty}\left(a-\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}\right)=a-1\ne0\)

\(\Rightarrow\lim\limits_{x\rightarrow+\infty}x\left(a-\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}\right)=\infty\) ko thỏa mãn giả thiết \(=4\) (hữu hạn)

\(\Rightarrow a=1\)

\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx-2}{x+\sqrt{x^2+bx+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-b-\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}}=-\dfrac{b}{2}\)

\(\Rightarrow-\dfrac{b}{2}=4\Rightarrow b=-8\)

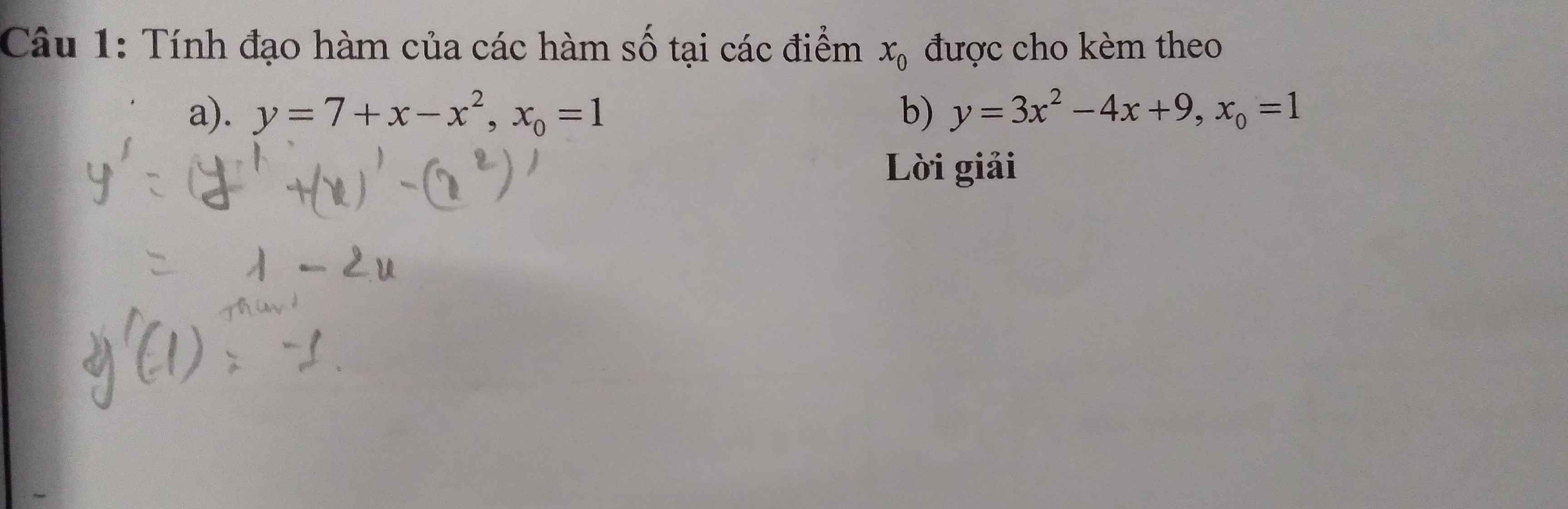
\(y'=\left(3x^2\right)'-\left(4x\right)'+9'\)

\(y'=6x-4\Rightarrow y'\left(1\right)=6.1-4=2\)

\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{mx^2-\left(m+3\right)x+3}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(mx-3\right)}{x-1}\)

\(=\lim\limits_{x\rightarrow1}\left(mx-3\right)=m-3\)

\(f\left(1\right)=m^2-15\)

Hàm liên tục tại \(x=1\) khi:

\(m-3=m^2-15\Rightarrow m^2-m-12=0\Rightarrow\left[{}\begin{matrix}m=4\\m=-3\end{matrix}\right.\)

\(4^2+\left(-3\right)^2=25\)

\(y'=3x^2-2\)

hệ số góc tiếp tuyến tại điểm có hoành độ \(x_0=-1\) là \(y'\left(-1\right)\)

\(y'\left(-1\right)=3.\left(-1\right)^2-2=1\)

14.

A là khẳng định sai, CD không vuông góc SB

(Vì nếu \(CD\perp SB\)  (1); do \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\) (2)

(1);(2) \(\Rightarrow CD\perp\left(SAB\right)\Rightarrow CD\perp AB\) (vô lý do \(CD||AB\))

\(f\left(x\right)=x^5+x^3\Rightarrow f'\left(x\right)=5x^4+3x^2\)

\(f'\left(2\right)=5.2^4+3.2^2=92\)

\(f\left(x\right)=x^5+x^3\)

=>\(f'\left(x\right)=5x^4+3x^2\)

=>\(f'\left(2\right)=5.2^4+3.2^2\)

\(f'\left(2\right)=5.16+3.4=92\)