Tập nghiệm của bất phương trình \(\dfrac{\text{x}^2-1}{x^2+x+1}>0\) là:
A. \(\left(1;+\infty\right)\) B. \(\left(-\infty;1\right)\) C. \(\left(-\infty;-1\right)\cup\left(1;+\infty\right)\) D. (-1; 1)
Những câu hỏi liên quan
Tập nghiệm của bất phương trình -x2 + 4x - 3 < 0 là:
A. \(\left(-\infty;1\right)\cup\left(3;+\infty\right)\) B. (1; 3) C. \(\text{∀}\text{x}\in\text{R}\) D. \(\left(-1;1\right)\)
Xem thêm câu trả lời
Biểu diễn hình học miền nghiệm của bất phương trình, hệ bất phương trình sau
1) \(3x-y+1>0\) 2) \(2\left(x-1\right)+y-2\le x-3y+1\)
8 tháng 3 2022 lúc 14:10
Biểu diễn hình học miền nghiệm của bất phương trình, hệ bất phương trình sau
1) 3x − y + 1 > 0 2) 2(x − 1) + y − 2 ≤ x − 3y + 1
Điều kiện xác định của bất phương trình \(\dfrac{\sqrt{\text{x}-2}}{x+1}-\sqrt{4-x}\ge0\) là:
A. \((-\infty;4]\backslash\left\{-1\right\}\) B. [2; +∞) C. \(\left[2;4\right]\) D. \([-1;4)\)
Xem thêm câu trả lời
Giải các bất phương trình sau
1) \(\sqrt{\text{x}^2+1}< 3\) 2) \(\dfrac{\text{x^2}-4x+3}{x^2-4}< 0\)
\(1)\sqrt{x^2+1}< 3.\\ \Leftrightarrow x^2+1< 9.\\ \Leftrightarrow x^2< 8.\\ \Leftrightarrow\left[{}\begin{matrix}x< 2\sqrt{2}.\\x>-2\sqrt{2}.\end{matrix}\right.\)
\(\Leftrightarrow-2\sqrt{2}< x< 2\sqrt{2}.\)
\(2)\dfrac{x^2-4x+3}{x^2-4}< 0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-4x+3}{x^2-4}.\)
\(x^2-4=0.\Leftrightarrow\left[{}\begin{matrix}x=2.\\x=-2.\end{matrix}\right.\\ x^2-4x+3=0.\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=1.\end{matrix}\right.\)
Bảng xét dấu:
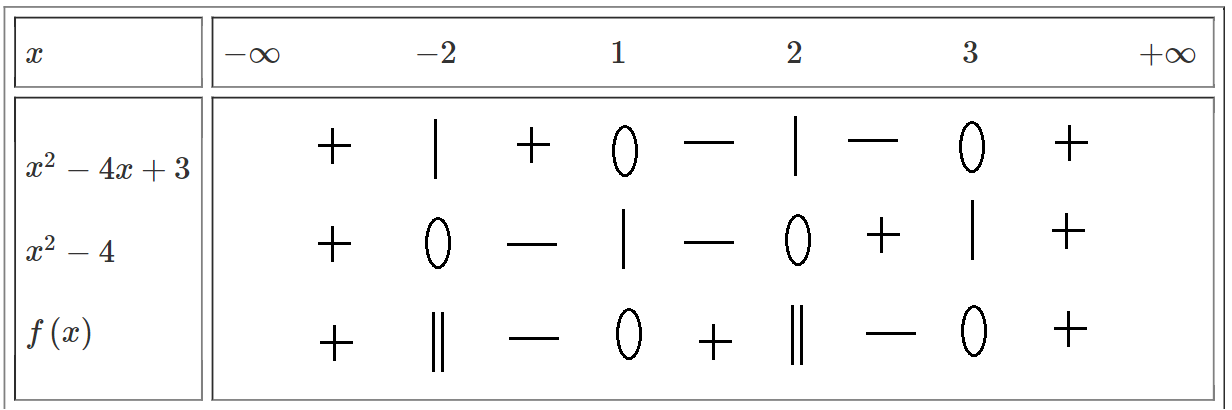
\(\Rightarrow f\left(x\right)< 0\Leftrightarrow x\in\left(-2;1\right)\cup\left(2;3\right).\)
Đúng 1
Bình luận (0)
Lời giải:
1.
$\sqrt{x^2+1}<3$
$\Leftrightarrow 0\leq x^2+1<9$
$\Leftrightarrow x^2+1<9$
$\Leftrightarrow x^2<8$
$\Leftrightarrow -2\sqrt{2}< x< 2\sqrt{2}$
2.
Xét 2 TH:
TH1: \(\left\{\begin{matrix} x^2-4x+3<0\\ x^2-4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x-1)(x-3)<0\\ (x-2)(x+2)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 1< x< 3\\ x>2 \text{hoặc} x<-2\end{matrix}\right.\)
\(\Leftrightarrow 2< x<3\)
TH2: \(\left\{\begin{matrix} x^2-4x+3>0\\ x^2-4<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x-1)(x-3)>0\\ (x-2)(x+2)<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>3 \text{hoặc} x<1\\ -2< x< 2\end{matrix}\right.\)
\(\Leftrightarrow -2< x< 1\)
Kết hợp 2 TH suy ra tập nghiệm \(S=(2;3)\cup (-2;1)\)
Đúng 0
Bình luận (0)
Bất phương trình: \(\sqrt{\text{-x^2 + 6x - 5}}>8-2x\) có nghiệm là:
A. 3 < x ≤ 5 B. 2 < x ≤ 3 C. -5 < x ≤ -3 D. -3 < x ≤ -2
Cho bất phương trình :
1
-
x
(
m
x
-
2
)
0
(
*
)
Xét các mệnh đề sau: (1) Bất phương trình tương đương với mx - 2 0 (2) m ≥ 0 là điều kiện cần để mọi x 1 là nghiệm của bất phương trình (*) (3) Với m 0 , tập nghiệm của bất phương trình là 2/m x 1 Mệnh...
Đọc tiếp
Cho bất phương trình : 1 - x ( m x - 2 ) < 0 ( * ) Xét các mệnh đề sau:
(1) Bất phương trình tương đương với mx - 2 <0
(2) m ≥ 0 là điều kiện cần để mọi x< 1 là nghiệm của bất phương trình (*)
(3) Với m < 0 , tập nghiệm của bất phương trình là 2/m< x< 1
Mệnh đề nào đúng?
A. Chỉ (1)
B. Chỉ (3)
C. (2) và (3)
D. Tất cả đúng
7 tháng 3 2022 lúc 22:41
Giải bất phương trình
1) \(\dfrac{3}{x-1}+2>0\) 2) \(\dfrac{1}{3x+1}-2\le0\)
1: \(\Leftrightarrow\dfrac{3+2x-2}{x-1}>0\)
\(\Leftrightarrow\dfrac{2x+1}{x-1}>0\)
=>x>1 hoặc x<-1/2
2: \(\Leftrightarrow\dfrac{1-6x-2}{3x+1}< =0\)
\(\Leftrightarrow\dfrac{6x+1}{3x+1}>=0\)
=>x>1/3 hoặc x<=-1/6
Đúng 1
Bình luận (0)
Cho bất phương trình :
1
-
x
(
mx
-
2
)
0
(
*
)
Xét các mệnh đề sau: (I) Bất phương trình tương đương với mx - 2 0; (II) m ≥ 0 là điều kiện cần để mọi x 1 là nghiệm của bất phương trình (*) (III) Với m 0 , tập nghiệm của bất phương trình là
2...
Đọc tiếp
Cho bất phương trình : 1 - x ( mx - 2 ) < 0 ( * )
Xét các mệnh đề sau:
(I) Bất phương trình tương đương với mx - 2 < 0;
(II) m ≥ 0 là điều kiện cần để mọi x < 1 là nghiệm của bất phương trình (*)
(III) Với m < 0 , tập nghiệm của bất phương trình là 2 m < x < 1
Mệnh đề nào đúng?
A. Chỉ (I)
B. Chỉ (III)
C. (II) và (III)
D. Cả (I), (II), (III)
