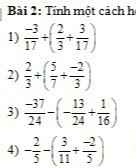 nhanh nhé hứa tick đúng
nhanh nhé hứa tick đúng

Những câu hỏi liên quan
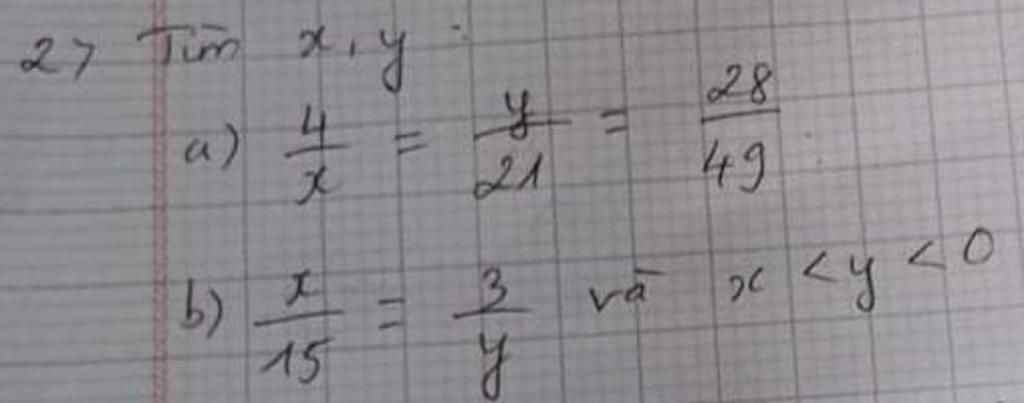 nhanh nhé hứa tick đúng
nhanh nhé hứa tick đúng
\(y=\dfrac{28.21}{49}=12\\ x=\dfrac{4.21}{12}=7\)
Đúng 0
Bình luận (0)
khi nào 8 - 2 = 10
ai nhanh mik hứa sẽ tick cho mà phải đúng nhé
8 - 2 = tam - 2 = ta -2 = 12 - 2 = 10
chuc bn hãc giài cac bn kb voi minh nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
 nhanh nhé mik gấp trước 9:45Ai nhanh mình tick liền cho mình hứa 100% luôn mik hứa
nhanh nhé mik gấp trước 9:45Ai nhanh mình tick liền cho mình hứa 100% luôn mik hứa
1 a lot
2 There
3 rivers
4 South
5 longest
6 than
7 in
8 highest
9 high
10 has
Đúng 2
Bình luận (0)
1.lots
2. There
3. rivers
4. South
5.long
6.than
7. to
8.highest
9. high
10.has
Đúng 2
Bình luận (0)
1.lots
2. There
3. rivers
4. South
5.long
6.than
7. to
8.highest
9. height
10.has
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp đi. Cần gấp trong tối nay. Hứa ko quỵt tick nè. Đảm bảo bài đúng, nhiều người tick đúng nè, nhanh nè Yên tâm đi ko nhanh hay là nhiều tick cx đc. Nhưng chỉ trong tối nay. Bài đúng và nhanh thì mình hứa sẽ tick ✔ và duyệt bạn í
CMR: tích của 4 số liên tiếp là một số chính phương.
Mn ơi! Nhanh chân lên!
Mk hứa sẽ tick 3 tick cho bn nào giải đúng.
Ghi rõ lời giải nhé
Gọi 4 số đó lần lượt là: n; n+1;n+2;n+3(n\(\inℕ\))
Theo đề bài ta có:
\(n\left(n+1\right)\left(n+2\right)\left(n+3\right)+1=n\left(n+3\right)\left(n+2\right)\left(n+1\right)+1\)
\(=\left(n^2+3n\right)\left(n^2+3n+2\right)+1\)
\(=\left(n^2+3n+1\right)^2\)
Mà n \(\inℕ\Rightarrow\left(n^2+3n+1\right)^2\inℕ\)
Vậy tích của 4 số n;n+1;n+2;n+3 là một số chính phương(đpcm)
Đúng 1
Bình luận (0)
Hứa tick cho ai đúng và nhanh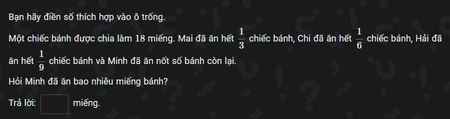
Ai giúp mk với
Hứa Tick nhanh cho bn đúng nek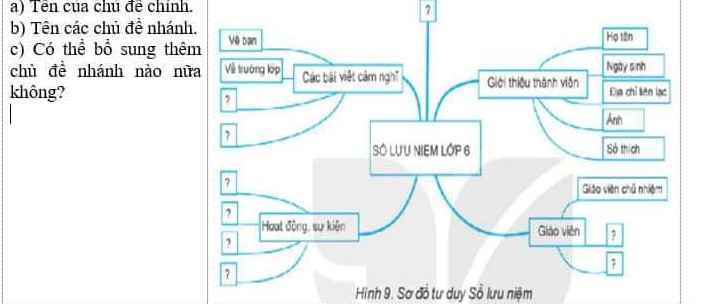
a) Chủ đề chính : SỔ LƯU NIỆM LỚP 6
b) Chủ đề nhánh: Giới thiệu thành viên, Hoạt động sự kiện, Các bài viết cảm nghĩ, Giáo viên.
d) Có
=> cụ thể : bổ sung thêm ở nhánh "?"
Đúng 1
Bình luận (0)
2,3<x>2,4
Giải nhanh hộ mình nha. Hứa là mình sẽ chọn ( Tick ) cho bạn trả lời chi tiết và đúng nhé. 10h là mình phải xong rồi nên làm ơn giúp mình nha! Please!Please!
2,3 còn gọi dc là 2.30 cũng ko thay đổi giá trị nên x có thể là:
2.31
2.32
2.33
2.34
2.35
2.36
2.37
2.38
2.39
thỏa mãn đề bài
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính nhanh
A= 1/1x2x3 + 1/2x3x4 + 1/3x4x5 +...+ 1/98x99x100
nhanh nhé hứa tick 15 đúng ạ
`A=1/[1xx2xx3]+1/[2xx3xx4]+1/[3xx4xx5]+....+1/[98xx99xx100]`
`A=1/2xx(2/[1xx2xx3]+2/[2xx3xx4]+2/[3xx4xx5]+....+2/[98xx99xx100])`
`A=1/2xx(1/[1xx2]-1/[2xx3]+1/[2xx3]-1/[3xx4]+1/[3xx4]-1/[4xx5]+....+1/[98xx99]-1/[99xx100])`
`A=1/2xx(1/[1xx2]-1/[99xx100])`
`A=1/2xx(1/2-1/9900)`
`A=1/2xx(4950/9900-1/9900)`
`A=1/2xx4949/9900`
`A=4949/19800`
Đúng 4
Bình luận (1)
\(A=\dfrac{3-1}{1.2.3}+\dfrac{4-2}{2.3.4}+\dfrac{5-3}{3.4.5}+...+\dfrac{100-98}{98.99.100}\)
\(A=\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{98.99}-\dfrac{1}{99.100}\right):2\)
\(A=\left(\dfrac{1}{2}-\dfrac{1}{6}+\dfrac{1}{12}-\dfrac{1}{20}+...+\dfrac{1}{9702}-\dfrac{1}{990}\right):2\)
\(A=\left(\dfrac{1}{2}-\dfrac{1}{990}\right):2\)
\(A=\dfrac{4949}{9900}:2\)
\(A=\dfrac{4949}{19800}\)
Đúng 2
Bình luận (1)






























