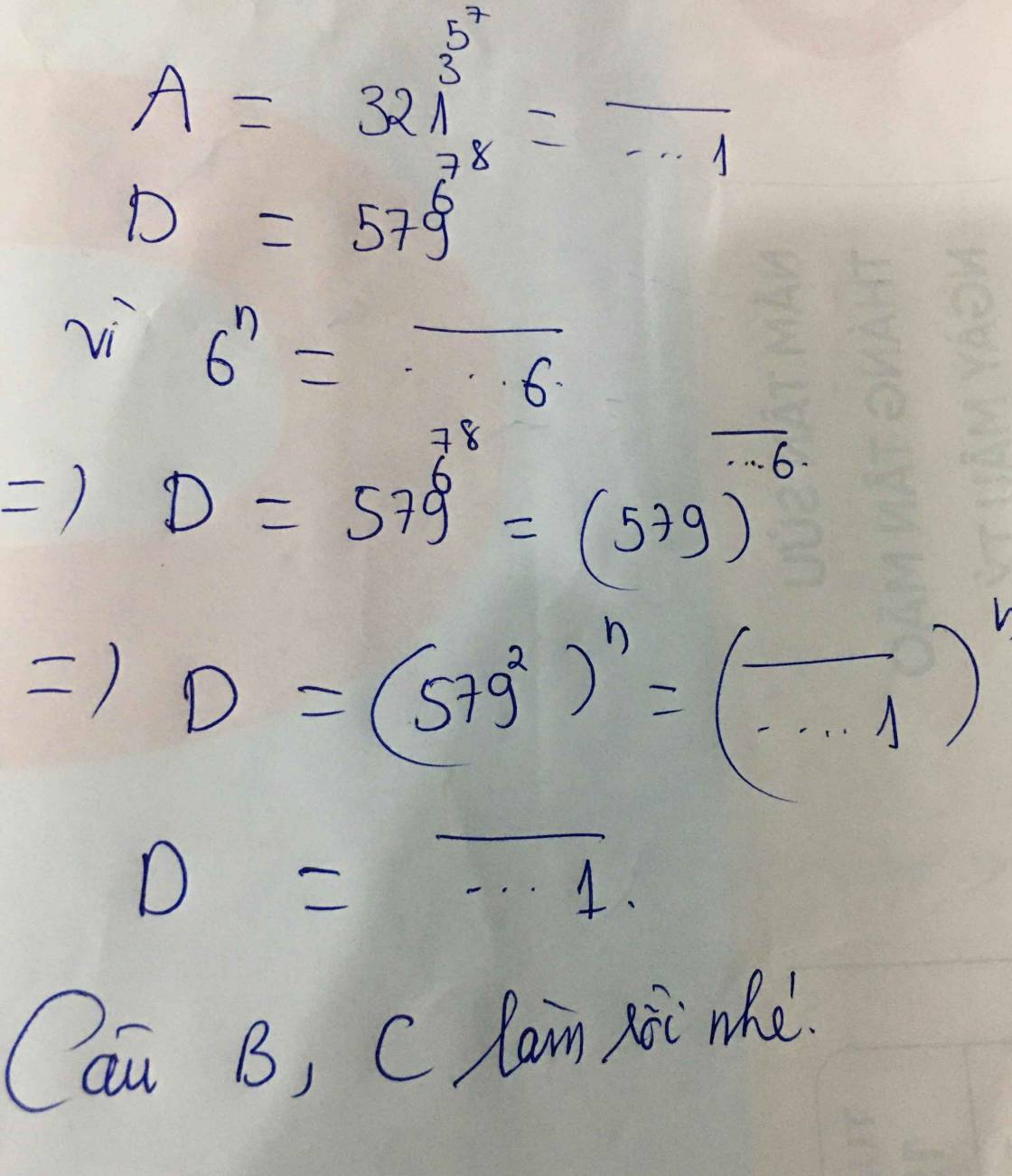-7/2022.503/3+7/2022.-508/3+7/3.(-2022)^0

Những câu hỏi liên quan
3^(x+2)+2022^0=(-4).(-7)
\(3^{x+2}+1=28\)
<=> \(3^{x+2}=27\)
<=> \(3^{x+2}=3^3\)
<=> x+2 = 3
<=> x =1
Đúng 2
Bình luận (0)
a) Tính giá trị biểu thức: 2^3 . 3^2 + 7^16 : 7^14 -2022^0
b) Tìm x biết: 2x-9=3 . (-7)
a) $2^3\cdot3^2+7^{16}:7^{14}-2022^0$
$=8\cdot9+7^2-1$
$=72+49-1$
$=120$
b) $2x-9=3\cdot(-7)$
$\Rightarrow2x-9=-21$
$\Rightarrow2x=-21+9$
$\Rightarrow2x=-12$
$\Rightarrow x=-12:2=-6$
Đúng 1
Bình luận (0)
Tìm lim (\(\dfrac{2021}{n^2}-\left(\dfrac{3}{7}\right)^n+2022\))
A. 2022 B.0 c.\(\infty\) d.-\(\infty\)
Tính B = \(13x^7-5y^3+2022\) tại x,y thỏa mãn: \(\left|x-1\right|+\left(y+2\right)^{2022}=0\)
\(\left|x-1\right|+\left(y+2\right)^{2022}=0\\ \Rightarrow\left\{{}\begin{matrix}\left|x-1\right|=0\\\left(y+2\right)^{2022}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x-1=0\\y+2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\\ \Rightarrow B=13.1-5\left(-8\right)+2022=13+40+2022=2075\)
Đúng 0
Bình luận (0)
|x-1|+(y+2)2022=0
Do |x-1| và (y+2)2022 đều ≥0⇒\(\left\{{}\begin{matrix}x-1=0\\y+2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
⇒B=13.(1)7-5.(-2)3+2022=13+40+2022=2075
Đúng 0
Bình luận (0)
Bài1:Thực hiện phép tính:
a,(2^4.3.5^2):{450:[450-(4.5^3-2^3.5^2)]}
b,3^3.5^2-20{90-[164-2.(7^8:7^6+7^0)]}
c,[(18^7:18^6-17).2022-1986].5.1^2022-13^2.2020^0
Bài2:Tìm x:
a,(2^x+1)^2+3.(2^2+1)=2^2.10
b,3.(x-7)+2.(x+5)=41
(GIÚP MIK VỚI Ạ)
Bài 1.
\(a,\left(2^4\cdot3\cdot5^2\right):\left\{450:\left[450-\left(4\cdot5^3-2^3\cdot5^2\right)\right]\right\}\)
\(=\left(16\cdot3\cdot25\right):\left\{450:\left[450- \left(4\cdot125-8\cdot25\right)\right]\right\}\)
\(=\left(48\cdot25\right):\left\{450:\left[450-\left(500-200\right)\right]\right\}\)
\(=1200:\left[450:\left(450-300\right)\right]\)
\(=1200:\left(450:150\right)\)
\(=1200:3\)
\(=400\)
\(---\)
\(b,3^3\cdot5^2-20\left\{90-\left[164-2\cdot\left(7^8:7^6+7^0\right)\right]\right\}\)
\(=27\cdot25-20\left\{90-\left[164-2\cdot\left(7^2+1\right)\right]\right\}\)
\(=675-20\left\{90-\left[164-2\cdot\left(49+1\right)\right]\right\}\)
\(=675-20\left[90-\left(164-2\cdot50\right)\right]\)
\(=675-20\left[90-\left(164-100\right)\right]\)
\(=675-20\left(90-64\right)\)
\(=675-20\cdot26\)
\(=675-520\)
\(=155\)
\(---\)
\(c,\left[\left(18^7:18^6-17\right)\cdot2022-1986\right]\cdot5\cdot1^{2022}-13^2\cdot2020^0\)
\(=\left[\left(18-17\right)\cdot2022-1986\right]\cdot5\cdot1-169\cdot1\)
\(=\left(1\cdot2022-1986\right)\cdot5-169\)
\(=\left(2022-1986\right)\cdot5-169\)
\(=36\cdot5-169\)
\(=180-169\)
\(=11\)
Bài 2.
\(a) (2^x+1)^2+3\cdot(2^2+1)=2^2\cdot10\\\Rightarrow (2^x+1)^2+3\cdot(4+1)=4\cdot10\\\Rightarrow (2^x+1)^2+3\cdot5=40\\\Rightarrow (2^x+1)^2+15=40\\\Rightarrow (2^x+1)^2=40-15\\\Rightarrow (2^x+1)^2=25\\\Rightarrow (2^x+1)^2= (\pm 5)^2\\\Rightarrow \left[\begin{array}{} 2^x+1=5\\ 2^x+1=-5 \end{array} \right.\\ \Rightarrow \left[\begin{array}{} 2^x=4\\ 2^x=-6 (vô.lí) \end{array} \right. \\ \Rightarrow 2^x=2^2\\\Rightarrow x=2\)
Vậy \(x=2\).
\(---\)
\(b)3\cdot(x-7)+2\cdot(x+5)=41\\\Rightarrow 3\cdot x+3\cdot(-7)+2\cdot x+2\cdot5=41\\\Rightarrow 3x-21+2x+10=41\\\Rightarrow (3x+2x)+(-21+10)=41\\\Rightarrow 5x-11=41\\\Rightarrow 5x=41+11\\\Rightarrow 5x=52\\\Rightarrow x=\dfrac{52}{5}\)
Vậy \(x=\dfrac{52}{5}\).
\(Toru\)
Đúng 4
Bình luận (0)
[ 155 - 15 . ( 2 . 5^2 - 3 . 4^2)] : ( 12 - 7 )^3 + 2022^0
[155 - 15.(2.52 - 3.42)] : (12 - 7)3 + 20220
= [155 - 15.(2.25 - 3.16)] : 53 + 1
= [155 - 15.(50 - 48)] : 125 + 1
= [155 - 15.2] : 125 + 1
= [155 - 30] : 125 +1
= 125 : 125 + 1
= 1 + 1
= 2
Đúng 2
Bình luận (0)
2³×3²+7¹⁶×7¹⁴-2022⁰
23.32 + 716.714 - 20220
= 25 + 730 - 1
Đúng 1
Bình luận (0)
3/2022-7/2x4-7/4x6-...-7/2020x202
tìm chữ số tận cùng của các số sau :
a) 321^3^5^7 b) 2022^2022
c) 234^5^6^7 d) 579^6^7^8