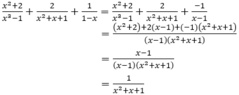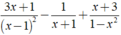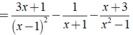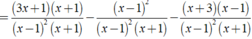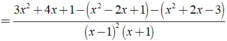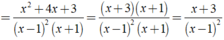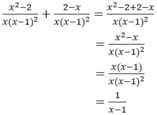Thực hiện phép tính: (1-x)(1-x2 )(1-x2.2)...(1-x2.10)

Những câu hỏi liên quan
Thực hiện phép tính
(
x
2
+
x
+
1
)
(
x
3
–
x
2
+
1
)
ta được kết quả là: A.
x
5
+ x + 1 B.
x
5
...
Đọc tiếp
Thực hiện phép tính ( x 2 + x + 1 ) ( x 3 – x 2 + 1 ) ta được kết quả là:
A. x 5 + x + 1
B. x 5 – x 4 + x
C. x 5 + x 4 + x
D. x 5 – x – 1
( x 2 + x + 1 ) ( x 3 – x 2 + 1 ) = x 2 . x 3 – x 2 . x 2 + x 2 . 1 + x . x 3 – x . x 2 + x . 1 + 1 . x 3 – 1 . x 2 + 1 . 1 = x 5 – x 4 + x 2 + x 4 – x 3 + x + x 3 – x 2 + 1 = x 5 + x + 1
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Thực hiện phép tính x 2 + 2 x 3 - 1 + 2 x 2 + x + 1 + 1 1 - x
Câu 2.(1,0 điểm) Thực hiện phép tính.
a) x + 1/5 . 10x/x2-1 b)1/ x+2 + x+6/x2-4
b: \(=\dfrac{x-2+x+6}{\left(x-2\right)\left(x+2\right)}=\dfrac{2}{x-2}\)
Đúng 0
Bình luận (0)
Thực hiện các phép tính sau:
3
x
+
1
(
x
-
1
)
2
-
1
x
+
1
+
x
+
3
1
-...
Đọc tiếp
Thực hiện các phép tính sau: 3 x + 1 ( x - 1 ) 2 - 1 x + 1 + x + 3 1 - x 2
Thực hiện các phép tính sau:
a) (x3 – 8) : (x – 2)
b) (x – 1)(x + 1)(x2 + 1)
a)

b) (x – 1)(x + 1)(x2 + 1)
= [x .(x + 1) – 1 .(x + 1)] . (x2 + 1)
= {x.x + x.1 + (-1).x + (-1).1}. (x2 + 1)
= (x2 + x – x – 1) . (x2 + 1)
= (x2 – 1) . (x2 + 1)
= x2 . (x2 +1) – 1.(x2 + 1)
= x2 . x2 + x2 . 1 – (1.x2 + 1.1)
= x4 + x2 – (x2 + 1)
= x4 + x2 – x2 – 1
= x4 – 1
Đúng 0
Bình luận (0)
thực hiện phép tính:
(-2x-1). (x2+5x-3)-(x-1)3
(-2x - 1)(x2 + 5x - 3) - (x - 1)3
= -2x3 - 10x2 + 6x - x2 - 5x + 3 - x3 + 3x2 - 3x + 1
= -3x3 - 8x2 - 2x + 4
Đúng 2
Bình luận (0)
Thực hiện phép tính x 2 - 2 x ( x - 1 ) 2 + 2 - x x ( x - 1 ) 2
Thực hiện các phép tính:
b
)
B
x
–
1
3
–
4
x
(
x
+
1
)
(
x
–
1
)
+
3
(...
Đọc tiếp
Thực hiện các phép tính:
b ) B = x – 1 3 – 4 x ( x + 1 ) ( x – 1 ) + 3 ( x – 1 ) ( x 2 + x + 1 )
b)B = x3 – 3x2 + 3x – 1 – 4x(x2 – 1) + 3(x2 – 1)
= x3 – 3x2 + 3x – 1 – 4x3 + 4 + 3x2 – 3 = -3x2 + 7x – 4
Đúng 0
Bình luận (0)
Thực hiện phép tính:
1)(x+x2-6):(x+3)
2)(x+x2-30):(x+6)
3)(5-3x+6x2):(2x-1)
\(1,=\left(x+3\right)\left(x-2\right):\left(x+3\right)=x-2\\ 2,=\left(x-5\right)\left(x+6\right):\left(x+6\right)=x-5\\ 3,=\left[3x\left(2x-1\right)-5\right]:\left(2x-1\right)=3x.dư.\left(-5\right)\)
Đúng 4
Bình luận (0)
1)\(\left(x+x^2-6\right):\left(x+3\right)=\left[x\left(x+3\right)-2\left(x+3\right)\right]:\left(x+3\right)=\left[\left(x+3\right)\left(x-2\right)\right]:\left(x+3\right)=x-2\)
2) \(\left(x+x^2-30\right):\left(x+6\right)=\left[x\left(x+6\right)-5\left(x+6\right)\right]:\left(x+6\right)=\left[\left(x+6\right)\left(x-5\right)\right]:\left(x+6\right)=x-5\)
3) \(\left(5-3x+6x^2\right):\left(2x-1\right)=\left[3x\left(2x-1\right)+5\right]:\left(2x-1\right)=3x+\dfrac{5}{2x-1}\)
Đúng 2
Bình luận (0)
Thực hiện phép tính
1/x+2 + 5/2x2+3x-2
-3x2/x3+11 + 1/x2-x+1 +1/x+1
1/1-x +1/1+x +2/1+x2 +4/1+x4
a) \(\dfrac{1}{x+2}+\dfrac{5}{2x^2+3x-2}\)
\(=\dfrac{1}{x+2}+\dfrac{5}{2x^2+4x-x-2}\)
\(=\dfrac{2x-1}{\left(2x-1\right)\left(x+2\right)}+\dfrac{5}{2x\left(x+2\right)-\left(x+2\right)}\)
\(=\dfrac{2x-1+5}{\left(2x-1\right)\left(x+2\right)}\)
\(=\dfrac{2x+4}{\left(2x-1\right)\left(x+2\right)}\)
\(=\dfrac{2\left(x+2\right)}{\left(2x-1\right)\left(x+2\right)}\)
\(=\dfrac{2}{2x-1}\)
\(---\)
b) \(\dfrac{-3x^2}{x^3+1}+\dfrac{1}{x^2-x+1}+\dfrac{1}{x+1}\) (sửa đề)
\(=\dfrac{-3x^2}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{-3x^2+x+1+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{-2x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{-2\left(x^2-1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{-2\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{-2x+2}{x^2-x+1}\)
\(---\)
c) \(\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)
\(=\dfrac{1+x}{\left(1-x\right)\left(1+x\right)}+\dfrac{1-x}{\left(1-x\right)\left(1+x\right)}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)
\(=\dfrac{1+x+1-x}{1^2-x^2}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)
\(=\dfrac{2}{1-x^2}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)
\(=\dfrac{2\left(1+x^2\right)}{\left(1-x^2\right)\left(1+x^2\right)}+\dfrac{2\left(1-x^2\right)}{\left(1-x^2\right)\left(1+x^2\right)}+\dfrac{4}{1+x^4}\)
\(=\dfrac{2+2x^2+2-2x^2}{1-x^4}+\dfrac{4}{1+x^4}\)
\(=\dfrac{4}{1-x^4}+\dfrac{4}{1+x^4}\)
\(=\dfrac{4\left(1+x^4\right)}{\left(1-x^4\right)\left(1+x^4\right)}+\dfrac{4\left(1-x^4\right)}{\left(1-x^4\right)\left(1+x^4\right)}\)
\(=\dfrac{4+4x^4+4-4x^4}{1-x^8}\)
\(=\dfrac{8}{1-x^8}\)
#\(Toru\)
Đúng 1
Bình luận (0)
\(\dfrac{1}{x+2}+\dfrac{5}{2x^2+3x-2}\\ =\dfrac{1}{x+2}+\dfrac{5}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2x-1}{\left(2x-1\right)\left(x+2\right)}+\dfrac{5}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2x-1+5}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2x+4}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2\left(x+2\right)}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2}{2x-1}\)
__
`x^3+1` chứ cậu nhỉ?
\(\dfrac{-3x^2}{x^3+1}+\dfrac{1}{x^2-x+1}+\dfrac{1}{x+1}\\ =\dfrac{-3x^2}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{1}{x^2-x+1}+\dfrac{1}{x+1}\\ =\dfrac{-3x^2}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x^2-x+1}{\left(x-1\right)\left(x^2-x+1\right)}\\ =\dfrac{-3x^2+x+1+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{-2x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{-2\left(x^2-1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{-2\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{-2\left(x-1\right)}{x^2-x+1}\)
__
Đúng 3
Bình luận (4)