bài này sử dụng định lí vi-ét nha

a.\(m=1\)

\(\Leftrightarrow x^2-2.1x+1^2-1-3=0\)

\(\Leftrightarrow x^2-2x-3=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\) ( Vi-ét )

b.\(\Delta=\left(-2m\right)^2-4\left(m^2-m-3\right)\)

      \(=4m^2-4m^2+4m+12\)

      \(=4m+12\)

Để pt có nghiệm kép thì \(\Delta=0\)

                                        \(\Leftrightarrow4m+12=0\) 

                                         \(\Leftrightarrow m=-3\)

Chọn D

Đặt  t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:

t²+ 2(1-m) t+ m²- 3 m+2= 0  (2)

Để pt (1) có nghiệm x ≥ 1 khi và chi khi pt (2) có nghiệm t ≥ 0

+ TH1: Pt (2) có nghiệm t₁ ≤ 0 ≤ t₂

Khi đó; P= t₁.t₂ ≤ 0 hay m²- 3m+ 2 ≤ 0

Từ đó; 1≤ m≤ 2

+ TH2: Pt (2) có nghiệm :

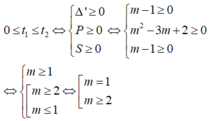
Kết luận: với  thì pt (1) có nghiệm x ≥ 1

Làm:-.-

Ta thấy x² -2mx +m²-m-6 =0 là phương trình bậc hai ẩn x

có : a=1, b=-2m \(\rightarrow\) b'= -m, c=m²-m-6

 \(\Rightarrow\Delta'=b'^2-ac=m^2-m^2+m+6=m+6\)

 Để phương trình có hai nghiệm x₁, x₂  phân biệt\(\Delta'>0\Leftrightarrow m+6>0\Leftrightarrow m>-6\)

Khi đó, phương trình có hai nghiệm phân biệt: 

 \(x_1=\dfrac{-b'-\sqrt{\Delta'}}{a}=m-\sqrt{m+6}\)

 \(x_2=\dfrac{-b'+\sqrt{\Delta'}}{a}=m+\sqrt{m+6}\)

mà \(\left|x_1\right|+\left|x_2\right|=8\) nên \(\left|m-\sqrt{m+6}\right|+\left|m+\sqrt{m+6}\right|=8\)

mà m>-6 nên 2m=8

                   \(\Leftrightarrow m=4\) (t/m)

Kl: m=4

giúp mình vớiii

Lời giải:
Để pt có 2 nghiệm thì:
$\Delta'=(m^2+2m)^2-(m^2+7)\geq 0$

$\Leftrightarrow m^4+4m^3+3m^2-7\geq 0(*)$
Áp dụng định lý Viet:

$x_1+x_2=2m(m+2)$

$x_1x_2=m^2+7$

Khi đó:

$x_1x_2-2(x_1+x_2)=4$

$\Leftrightarrow m^2+7-4m(m+2)=4$

$\Leftrightarrow -3m^2-8m+3=0$

$\Leftrightarrow (1-3m)(m+3)=0$

$\Leftrightarrow m=\frac{1}{3}$ hoặc $m=-3$

Thử lại với $(*)$ thấy đều không thỏa mãn

Vậy không tồn tại $m$ thỏa mãn đkđb

Phương trình đã cho có nghiệm phân biệt khi : 

\(\Delta'=m^2-\left(m^2+2m+3\right)=-2m-3>0\)

\(\Leftrightarrow m< -\dfrac{3}{2}\)(*)

Hệ thức Viette : \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=m^2+2m+3\end{matrix}\right.\)

Có \(x_1^3+x_2^3=108\)

\(\Leftrightarrow\left(x_1+x_2\right).\left(x_1^2-x_1x_2+x_2^2\right)=108\)

\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=108\)

\(\Leftrightarrow-8m^3+6m\left(m^2+2m+3\right)=108\)

\(\Leftrightarrow m^3-6m^2-9m+54=0\)

\(\Leftrightarrow\left(m-6\right).\left(m-3\right).\left(m+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=6\\m=\pm3\end{matrix}\right.\)

Kết hợp (*) được m = -3 thỏa mãn

Đáp án D

Để phương trình có nghiệm

\(\Delta'=\left(-m\right)^2-1.\left(m^2-\dfrac{1}{2}\right)\ge0\Leftrightarrow\dfrac{1}{2}\ge0\) ( luôn đúng)

Áp dụng vi.et có

\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-\dfrac{1}{2}\end{matrix}\right.\)

Theo bài ra ta có

\(x_1^2+x_2^2=9\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=9\)

\(\Leftrightarrow\left(2m\right)^2-2\left(m^2-\dfrac{1}{2}\right)=9\)

\(\Leftrightarrow4m^2-2m^2+1=9\)

\(\Leftrightarrow2m^2=8\Leftrightarrow m^2=4\Leftrightarrow m=\pm2\)

Để pt có nghiệm <=>  \(\Delta'\ge0\Leftrightarrow\left(-m\right)^2-1\left(m^2-\dfrac{1}{2}\right)\ge0\)

\(\Leftrightarrow m^2-m^2+\dfrac{1}{2}\ge0\Leftrightarrow\dfrac{1}{2}\ge0\) (Đúng)

Vậy pt luôn có 2 nghiệm x₁,x₂

Theo hệ thức vi-et, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-\dfrac{1}{2}\end{matrix}\right.\)

Ta có: \(x_1^2+x_2^2=3^2=9\)

<=>\(\left(x_1+x_2\right)^2-2x_1x_2=9\)

<=>(2m)²-2(m²-1/2)=9

<=>4m²-2m²+1=9

<=>2m²=8<=>m²=4<=>\(m=\pm2\)