cho (c) y= x^3 -3x +7 tìm phương trình tiếp tuyến biết tiếp tuyến tạo với d: y= 2x+3 một góc 45°

Những câu hỏi liên quan
Viết phương trình tiếp tuyến của đồ thị hàm số
y
3
x
-
2
x
-
1
. Biết tiếp tuyến tạo với trục hoành một góc
45
°
. A.
y
-
x
-
6
hoặc
y
-
x
-
2
B.
y...
Đọc tiếp
Viết phương trình tiếp tuyến của đồ thị hàm số y = 3 x - 2 x - 1 . Biết tiếp tuyến tạo với trục hoành một góc 45 ° .
A. y = - x - 6 hoặc y = - x - 2
B. y = - x + 6 hoặc y = x - 2
C. y = x + 6 hoặc y = x + 2
D. y = - x + 6 hoặc y = - x + 2
Đáp án D.
Tiếp tuyến tạo với trục hoành một góc 45 °

Đúng 1
Bình luận (0)
câu 1.cho đường tròn (c) : \(x^2+y^2+4x+4y-17=0\). viết phương trình tiếp tuyến của (C) biết tiếp tuyến tạo với Õ một góc \(60^0\)
câu 2. cho hai đường trong (c1)\(x^2+y^2-2x-2y=0\), (c2) \(x^2+y^2-4x-6y-3=0\) viết phương trình tiếp tuyến chung của 2 đường tròn
1.
Tạo với Ox là tạo với tia Ox hay trục hoành nhỉ? 2 cái này khác nhau đấy. Tạo với tia Ox thì chỉ có 1 góc 60 độ theo chiều dương, tạo với trục hoành thì có 2 góc 60 và 120 đều thỏa mãn. Coi như tạo tia Ox đi
Đường tròn tâm \(I\left(-2;-2\right)\) bán kính \(R=5\)
\(tan60^0=\sqrt{3}\Rightarrow\) tiếp tuyến có hệ số góc bằng \(\sqrt{3}\Rightarrow\) pt có dạng:
\(y=\sqrt{3}x+b\Leftrightarrow\sqrt{3}x-y+b=0\)
\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|-2\sqrt{3}+2+b\right|}{\sqrt{3+1}}=5\)
\(\Leftrightarrow\left|b+2-2\sqrt{3}\right|=10\Rightarrow\left[{}\begin{matrix}b=8+2\sqrt{3}\\b=-12+2\sqrt{3}\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}\sqrt{3}x-y+8+2\sqrt{3}=0\\\sqrt{3}x-y-12+2\sqrt{3}=0\end{matrix}\right.\)
Đúng 1
Bình luận (1)
2.
(C1) có tâm \(I\left(1;1\right)\) bán kính \(R_1=\sqrt{2}\)
(C2) có tâm \(J\left(2;3\right)\) bán kính \(R_2=4\)
Gọi tiếp tuyến chung d có pt: \(ax+by+c=0\)
\(\left\{{}\begin{matrix}d\left(I;d\right)=R_1\\d\left(J;d\right)=R_2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{\left|a+b+c\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\\\dfrac{\left|2a+3b+c\right|}{\sqrt{a^2+b^2}}=4\end{matrix}\right.\)
\(\Rightarrow2\sqrt{2}\left|a+b+c\right|=\left|2a+3b+c\right|\)
? Đề nghiêm túc đấy chứ? Cho kiểu này thì sấp mặt, tối thiểu pt (C1) cũng có dạng \(x^2+y^2-2x-2y+1=0\) để học sinh còn thở chứ.
Đúng 0
Bình luận (2)
Ủa, nhìn lại thì bài 2 người ta cho đề kiểu hack não.
\(\overrightarrow{IJ}=\left(1;2\right)\Rightarrow IJ=\sqrt{5}< R_2-R_1=4-\sqrt{2}\)
Do đó \(\left(C_2\right)\) chứa \(\left(C_1\right)\) nên ko tồn tại tiếp tuyến chung của 2 đường tròn
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Viết phương trình tiếp tuyến của đồ thị hàm số
y
3
x
−
2
x
−
1
. Biết tiếp tuyến tạo với trục hoành một góc
45
0
. A.
y
−
x
−
6
hoặc
y
−
x
−...
Đọc tiếp
Viết phương trình tiếp tuyến của đồ thị hàm số y = 3 x − 2 x − 1 . Biết tiếp tuyến tạo với trục hoành một góc 45 0 .
A. y = − x − 6 hoặc y = − x − 2
B. y = − x + 6 hoặc y = − x + 2
C. y = − x + 6 hoặc y = x − 2
D. y = x + 6 hoặc y = x + 2
Cho hàm số
y
3
x
-
2
x
-
2
.Viết phương trình tiếp tuyến d với đồ thị hàm số biết d tạo với trục hoành một góc α mà A. y -4x – 19, y -4x – 1. B. y -4x + 19, y -x + 3. C. y -4x + 19, y -4x + 3. D. Tất cả sai
Đọc tiếp
Cho hàm số
y
=
3
x
-
2
x
-
2
.Viết phương trình tiếp tuyến d với đồ thị hàm số biết d tạo với trục hoành một góc α mà 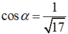
A. y = -4x – 19, y = -4x – 1.
B. y = -4x + 19, y = -x + 3.
C. y = -4x + 19, y = -4x + 3.
D. Tất cả sai
Chọn C.
Ta có : 
Gọi  là tiếp điểm của của tiếp tuyến và đồ thị hàm số.
là tiếp điểm của của tiếp tuyến và đồ thị hàm số.
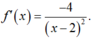
Trục hoành là đường thẳng có hệ số góc k1 = 0.
Gọi k2 là hệ số góc của tiếp tuyến cần tìm. Ta có: 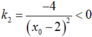
Ta có: 
Do đó: 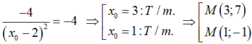
Với M(3; 7), pttt là: y = -4(x – 3) + 7 ⇒ y = -4x + 19.
Với M(1; -1), pttt là: y = -4(x – 1) – 1 ⇒ y = -4x + 3.
Có hai tiếp tuyến thỏa mãn ycbt là y = -4x + 3 và y = -4x + 19.
Đúng 0
Bình luận (0)
Cho hàm số
y
3
x
-
2
x
-
2
.Viết phương trình tiếp tuyến d với đồ thị hàm số biết d tạo với trục hoành một góc α mà
cos
α
1
17
A. 4x+y-30; 4x+y-190 B. 4x+y+30; 4x+y+190 C. 4x-y-30; 4x-y+190 D: Đáp án khác
Đọc tiếp
Cho hàm số y = 3 x - 2 x - 2 .Viết phương trình tiếp tuyến d với đồ thị hàm số biết d tạo với trục hoành một góc α mà cos α = 1 17
A. 4x+y-3=0; 4x+y-19=0
B. 4x+y+3=0; 4x+y+19=0
C. 4x-y-3=0; 4x-y+19=0
D: Đáp án khác
Viết phương trình tiếp tuyến của đường tròn (C) : (x-1)² + (y+1)² = 10 biết tiếp tuyến đó tạo với đường thẳng d: 2x + y - 4=0 một góc 45 độ
Mình cảm ơn nhiều!
gọi pt tiếp tuyến có dạng Ax+By+C=0, có 2 phương trình để tìm A,B,C là cos giữa 2 đt và d(I;d)=10−−√d(I;d)=10.xong rồi thế và chọn giá trị nhé ^^
Đúng 0
Bình luận (0)
Cho hàm số f(X)= x^2 +2x +1. Viết phương trình tiếp tuyến của f(x) , biết tiếp tuyến tạo với trục Ox một góc bằng 45 độ .
\(f'\left(x\right)=2x+2\)
Gọi \(x_0\) là hoành độ tiếp điểm, do tiếp tuyến tạo với trục Ox một góc 45 độ
\(\Rightarrow\) Tiếp tuyến có hệ số góc bằng 1 hoặc -1
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_0\right)=2x_0+2=1\\f'\left(x_0\right)=2x_0+2=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=-\dfrac{1}{2}\Rightarrow y_0=\dfrac{1}{4}\\x_0=-\dfrac{3}{2}\Rightarrow y_0=\dfrac{1}{4}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=1\left(x+\dfrac{1}{2}\right)+\dfrac{1}{4}\\y=-1\left(x+\dfrac{3}{2}\right)+\dfrac{1}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Viết phương trình tiếp tuyến \(\Delta\) với đồ thị (C) của hàm số \(y=x^3-x^2+x-1\) biết rằng tiếp tuyến \(\Delta\) tạo với đường thẳng \(d:3x+y-1=0\) một góc \(45^0\)
Gọi hệ số góc của \(\Delta\) là k \(\Rightarrow\overrightarrow{n_{\Delta}}=\left(k;-1\right);\overrightarrow{n_d}=\left(3;1\right)\)
Yêu cầu bài toán :
\(\Leftrightarrow\frac{\left|3k-1\right|}{\sqrt{1+k^2}.\sqrt{10}}=\frac{1}{\sqrt{2}}\)
\(\Leftrightarrow2k^2-3k-2=0\)
\(\Leftrightarrow k=-\frac{1}{2}\) hoặc k = 2
Từ đó ta có được 2 tiếp tuyến là \(y=2x-2;y=2x-\frac{22}{27}\)
Đúng 0
Bình luận (0)
1. Cho (P): y x2 - 3x + 2. Lập ft tiếp tuyến của (P) biết rằng :a. Tiếp tuyến đó tạo với Ox một góc bằng 45o.b. Tiếp tuyến đó song song với đường thẳng y 2x + 1.c. Tiếp tuyến đó vuông góc với đường thẳng y -frac{1}{3}frac{1}{3}x + 2.2. Tìm ft tiếp tuyến chung của 2 parabol (P) : y x2 + 4x + 8và (P) : y x2 + 8x + 4.
Đọc tiếp
1. Cho (P): y = x2 - 3x + 2. Lập ft tiếp tuyến của (P) biết rằng :
a. Tiếp tuyến đó tạo với Ox một góc bằng 45o.
b. Tiếp tuyến đó song song với đường thẳng y = 2x + 1.
c. Tiếp tuyến đó vuông góc với đường thẳng y = -\(\frac{1}{3}\)\(\frac{1}{3}\)
x + 2.
2. Tìm ft tiếp tuyến chung của 2 parabol (P) : y = x2 + 4x + 8
và (P') : y = x2 + 8x + 4.













