Mn giúp mik nốt bài này vs ạ!

Những câu hỏi liên quan
Giúp mik vs, nếu ai thấy đc bài này thì hãy giúp mik vs ạ. Mik camon mn
Mn giải giúp mik bài này vs ạ

1. What did the people do when you were there
2. I visited Dalat with my parents.
3. What do you think of Tam?
4. The life in countryside is peaceful and more than I expected
Đúng 1
Bình luận (0)
1.What did the people do when you were there?
2.I visited Da Lat with my parents.
3.What do you think of Tam?
4.The life in the countryside is more peaceful than I expected.
Đúng 1
Bình luận (0)
Ai lm nốt cho mik 2 bài này vs ạ

Mn ơi giúp mik giải bài này vs mik cần gấp ạ >
Giúp mik bài này vs ạ, chỉ cần cậ d thôi ạ( mn giúp em vs em đang cần gấp )
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
Đúng 0
Bình luận (0)
Mn làm giúp mik 2 bài này vs ạ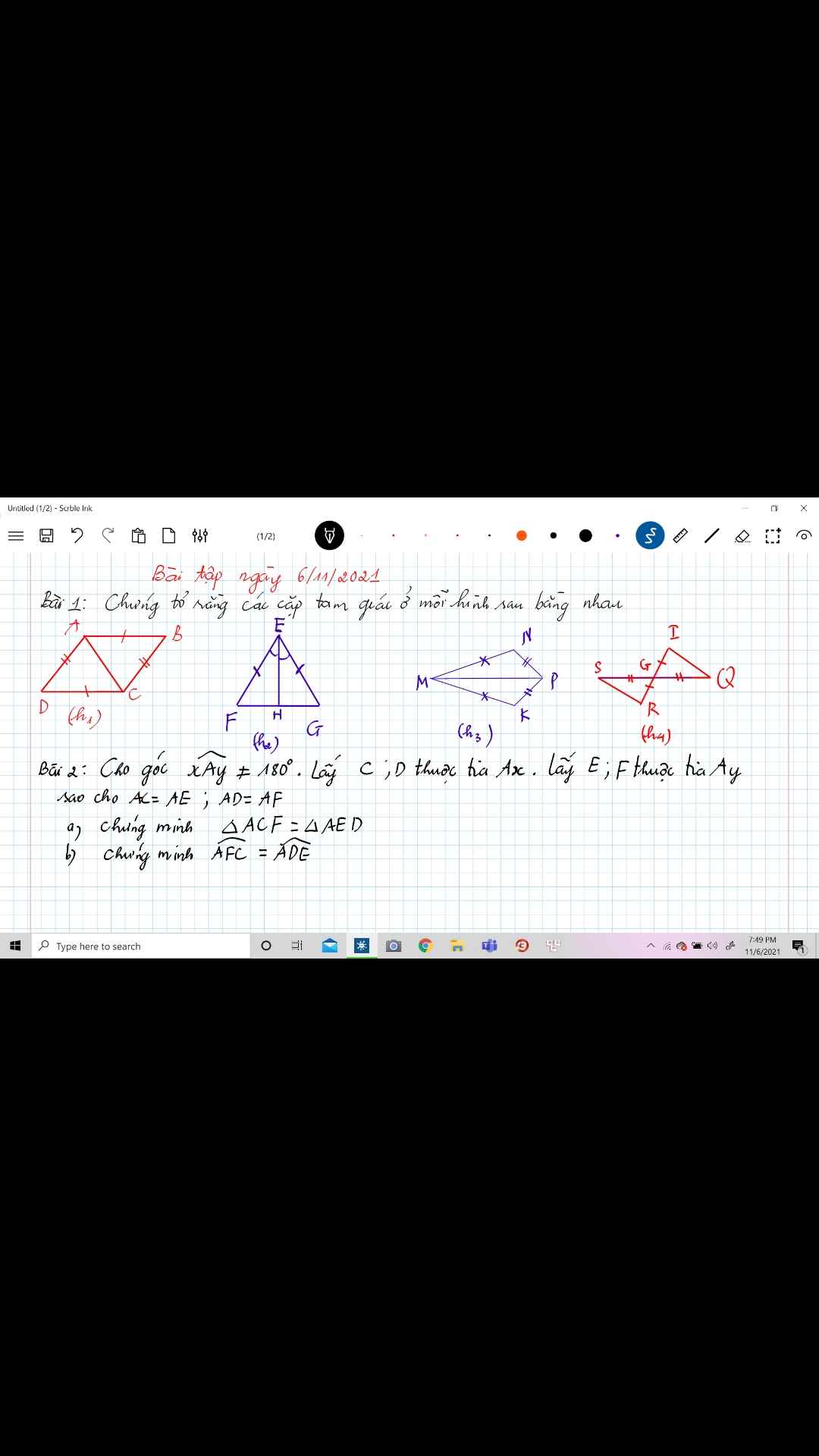
a: Xét ΔACF và ΔAED có
AC=AE
\(\widehat{A}\) chung
AF=AD
Do đó: ΔACF=ΔAED
Đúng 0
Bình luận (0)
Mn người giúp mik giải bài này vs ạ
Ta có \(\dfrac{1}{1.3}\)+\(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+...+\(\dfrac{1}{49.51}\)
=\(\dfrac{2}{2}\).(\(\dfrac{1}{1.3}\)+\(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+...+\(\dfrac{1}{49.51}\))
=\(\dfrac{1}{2}\).(\(\dfrac{2}{1.3}\)+\(\dfrac{2}{3.5}\)+\(\dfrac{2}{5.7}\)+...+\(\dfrac{2}{49.50}\))
=\(\dfrac{1}{2}\).(1-\(\dfrac{1}{3}\)+\(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{49}-\dfrac{1}{51}\))
=\(\dfrac{1}{2}\).(\(1-\dfrac{1}{51}\))
=\(\dfrac{1}{2}\).\(\dfrac{50}{51}\)
=\(\dfrac{25}{51}\)
Đúng 2
Bình luận (0)
Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{49\cdot51}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{49\cdot51}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{51}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{50}{51}=\dfrac{25}{51}\)
Đúng 1
Bình luận (0)
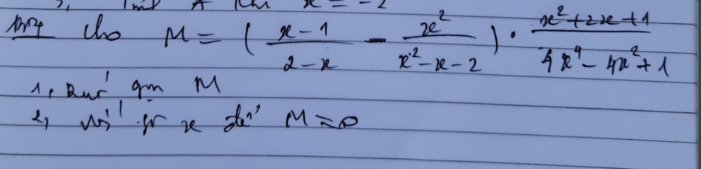
mn ơi giúp mik nốt câu này dc ko ạ plssss
1
Với \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\)
\(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\left(\dfrac{x^2+2x+1}{4x^4-4x^2+1}\right)\\ =\left(\dfrac{\left(x-1\right)\left(x+1\right)}{\left(2-x\right)\left(x+1\right)}+\dfrac{x^2}{\left(x+1\right)\left(2-x\right)}\right)\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{x^2-1+x^2}{\left(x+1\right)\left(2-x\right)}\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{\left(2x^2-1\right)\left(x+1\right)^2}{\left(x+1\right)\left(2-x\right)\left(2x^2-1\right)^2}\\ =\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}\)
2
Để M = 0 thì \(\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}=0\Rightarrow x+1=0\Rightarrow x=-1\) (loại)
Vậy không có giá trị x thỏa mãn M = 0
Đúng 2
Bình luận (0)
1) \(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\cdot\dfrac{x^2+2x+1}{4x^4-4x^2+1}\) (ĐK: \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\))
\(M=\left(\dfrac{-\left(x-1\right)}{x-2}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x^2-1\right)-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-x^2+1-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-2x^2+1}{\left(x-2\right)\left(x+1\right)}\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(2x^2-1\right)\left(x+1\right)^2}{\left(x-2\right)\left(x+1\right)\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}\)
2) Ta có: \(M=0\)
\(\Rightarrow\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}=0\)
\(\Leftrightarrow-\left(x+1\right)=0\)
\(\Leftrightarrow-x=1\)
\(\Leftrightarrow x=-1\left(ktm\right)\)
Đúng 1
Bình luận (0)
1: \(M=\left(\dfrac{-x+1}{x-2}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(=\dfrac{-x^2+1-x^2}{\left(x-2\right)\left(x+1\right)}\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(=\dfrac{1-2x^2}{\left(x-2\right)}\cdot\dfrac{x+1}{\left(1-2x^2\right)^2}=\dfrac{x+1}{\left(x-2\right)\left(1-2x^2\right)}\)
2: M=0
=>x+1=0
=>x=-1(loại)
Đúng 0
Bình luận (0)

giúp mik gải nốt bài này vs![]()
![]()
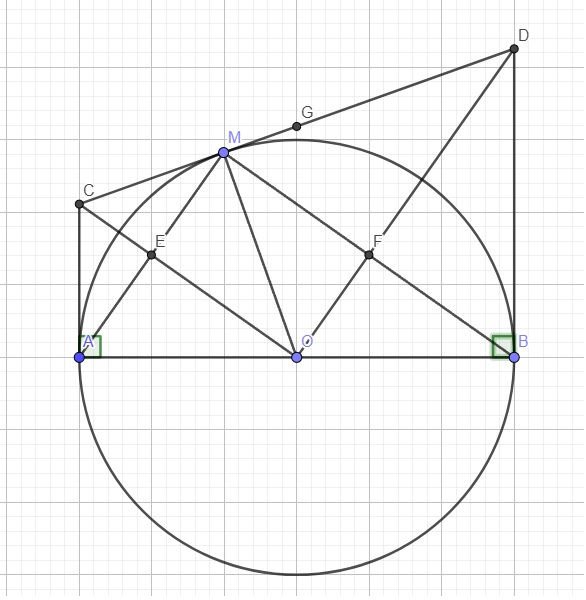
a.
Do C là giao điểm 2 tiếp tuyến tại A và M
\(\Rightarrow AC=MC\)
Tương tự có \(BD=MD\)
\(\Rightarrow AC+BD=MC+MD=CD\)
2.
Cũng theo t/c hai tiếp tuyến cắt nhau ta có:
\(\left\{{}\begin{matrix}\widehat{COA}=\widehat{COM}\\\widehat{DOB}=\widehat{DOM}\end{matrix}\right.\)
\(\Rightarrow\widehat{COA}+\widehat{COM}+\widehat{DOB}+\widehat{DOM}=2\left(\widehat{COM}+\widehat{DOM}\right)\)
\(\Rightarrow180^0=2\widehat{COD}\)
\(\Rightarrow\widehat{COD}=90^0\)
Hay tam giác COD vuông tại O
Trong tam giác vuông COD, do CD là tiếp tuyến tại M \(\Rightarrow OM\perp CD\)
\(\Rightarrow OM\) là đường cao ứng với cạnh huyền
Áp dụng hệ thức lượng:
\(OM^2=CM.MD\Rightarrow R^2=AC.BD\) (do \(AC=CM;BD=MD\))
Đúng 2
Bình luận (0)
3.1
Theo cmt ta có \(AC=MC\)
Lại có \(OA=OM=R\)
\(\Rightarrow OC\) là trung trực của AM
\(\Rightarrow OC\perp AM\) tại E
\(\Rightarrow\widehat{OEM}=90^0\)
Hoàn toàn tương tự ta có \(\widehat{OFM}=90^0\)
\(\Rightarrow OEMF\) là hình chữ nhật (tứ giác vó 3 góc vuông)
3.2
\(OM\perp CD\Rightarrow\Delta OCM\) vuông tại M
\(ME\perp OC\Rightarrow ME\) là đường cao trong tam giác vuông OCM
Áp dụng hệ thức lượng:
\(OM^2=OE.OC\Rightarrow OE.OC=R^2\)
Hoàn toàn tương tự ta có: \(OM^2=OF.OD\)
\(\Rightarrow OE.OC=OF.OD=R^2\)
3.3
Do OC là trung trực AM (chứng minh câu 3.1) \(\Rightarrow E\) là trung điểm AM
Tương tự ta có F là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác MAB
\(\Rightarrow EF||AB\)
Mà \(AB\perp BD\) (do BD là tiếp tuyến tại B)
\(\Rightarrow EF\perp BD\)
3.4
Gọi G là trung điểm CD.
Do tam giác COD vuông tại O (theo cm câu 2) \(\Rightarrow\) G là tam đường tròn ngoại tiếp tam giác COD
Hay \(GO\) là 1 bán kính của đường tròn đường kính CD (1)
\(CA\) và BD cùng vuông góc AB \(\Rightarrow CA||BD\Rightarrow ACDB\) là hình thang
O là trung điểm AB, G là trung điểm CD \(\Rightarrow OG\) là đường trung bình hình thang ACDB
\(\Rightarrow GO||DB\Rightarrow GO\perp AB\) tại G (2)
(1);(2)\(\Rightarrow AB\) là tiếp tuyến của đường tròn đường kính CD
Đúng 2
Bình luận (0)