TÌM BCNN(12;14;16)

Những câu hỏi liên quan
Tìm BCNN(8, 12); BCNN(5, 7, 8); BCNN(12, 16, 48).
* Tìm BCNN(8 ; 12) :
+ Phân tích thành thừa số nguyên tố :
8 = 23
12 = 22.3.
+ Các thừa số nguyên tố chung và riêng là : 2 ; 3.
⇒ BCNN(8 ; 12) = 23.3 = 24.
* Tìm BCNN(5 ; 7 ; 8)
+ Phân tích thành thừa số nguyên tố :
5 = 5
7 = 7
8 = 23.
+ Các thừa số nguyên tố chung và riêng : 2 ; 5 ; 7.
⇒ BCNN(5 ; 7 ; 8) = 23.5.7 = 280.
* Tìm BCNN(12 ; 16 ; 48).
+ Phân tích thành thừa số nguyên tố :
12 = 22.3
16 = 24
48 = 24.3.
+ Các thừa số nguyên tố chung và riêng : 2 ; 3.
⇒ BCNN(12; 16; 48) = 24.3 = 48.
Đúng 0
Bình luận (0)
Tìm BCNN của
a) BCNN (24, 10)
b) BCNN( 8, 12, 15)
a) BCNN (24, 10) = 120
b) BCNN ( 8, 12, 15) = 120
Đúng 0
Bình luận (0)
Tìm BCNN(24, 30); BCNN(3, 7, 8); BCNN(12, 16, 48).
- Ta có: 24 = 23.3
30 = 2.3.5
BCNN(24, 30) = 23.3.5 = 120
- Ta có các số 3, 7, 8 từng đôi một là số nguyên tố cùng nhau.
=> BCNN(3, 7, 8) = 3.7.8 = 168
- Ta có 48 là bội của 12 và 16
=> BCNN(12, 16, 48) = 48.
Đúng 1
Bình luận (0)
Tìm BCNN của 15 và 3
Tìm BCNN của 11;3 và 33
Tìm BCNN của 6;2 và 12
Tìm BCNN của 4;3 và 15
BCNN(15;3) = 15
BCNN(11;3;33) = 33
BCNN(6;2;12) = 36
BCNN(4;3;15) = 60
Đúng 0
Bình luận (0)
1) Tìm:a) BCNN (8, 20) b) BCNN (24; 45; 50). c)Tìm BCNN (90; 120; 180).2) Tìm BCNN rồi tìm BC của:a) 25 và 35 b) 36 và 40 c) 12; 18 và 303) Tìm số tự nhiên a nhỏ nhất khác 0 biết và 4) Tìm số tự nhiên x biết:a) và x 500 b) và 5) Số học sinh khối 6 của một trường THCS trong khoảng từ 400 đến 500 học sinh. Nếu xếp thành 8 hàng hay 10 hàng hay 12 hàng thì đều vừa đủ. Tính số học sinh khối...
Đọc tiếp
1) Tìm:
a) BCNN (8, 20) b) BCNN (24; 45; 50). c)Tìm BCNN (90; 120; 180).
2) Tìm BCNN rồi tìm BC của:
a) 25 và 35 b) 36 và 40 c) 12; 18 và 30
3) Tìm số tự nhiên a nhỏ nhất khác 0 biết ![]() và
và ![]()
4) Tìm số tự nhiên x biết:
a) ![]() và x < 500 b)
và x < 500 b) ![]() và
và ![]()
5) Số học sinh khối 6 của một trường THCS trong khoảng từ 400 đến 500 học sinh. Nếu xếp thành 8 hàng hay 10 hàng hay 12 hàng thì đều vừa đủ. Tính số học sinh khối 6 của trường đó?
6) Một số sách khi xếp thành từng bó 10 cuốn, 15 cuốn, 18 cuốn đều vừa đủ. Biết số sách trong khoảng từ 320 đến 400 cuốn. Tính số sách.
7) Số học sinh khối 6 của một trường khoảng từ 500 đến 600 học sinh. Khi xếp hàng 12, hàng 15, hàng 18 đều thừa 4 học sinh. Tính số học sinh khối 6.
8) Số học sinh khối 6 của một trường có từ 200 đến 400 em. Biết rằng khi xếp hàng 10; hàng 12; hàng 18 đều thiếu 3 em thì đủ hàng. Tính số học sinh khối 6.
9) Ba ô tô cùng khởi hành một lúc từ một bến. Thời gian cả đi lẫn về của xe thứ nhất là 40 phút, của xe thứ hai là 50 phút, của xe thứ ba là 30 phút. Khi trở về bến, mỗi xe đều nghỉ 10 phút rồi tiếp tục chạy. Hỏi sau ít nhất bao lâu thì cả ba xe cùng rời bến?
10) Tìm hai số tự nhiên có tích bằng 720 và có BCNN bằng 120.
Bài 1:
a: BCNN(8;20)=40
b: BCNN(24;45;50)=1800
Đúng 1
Bình luận (1)
Điền vào chỗ trống để quy đồng mẫu các phân số: - Tìm BCNN(12, 30): 12 22 . 3 30 ... BCNN(12, 30) … - Tìm thừa số phụ: … : 12 … … : 30 … - Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng:
Đọc tiếp
Điền vào chỗ trống để quy đồng mẫu các phân số:
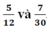
- Tìm BCNN(12, 30):
12 = 22 . 3
30 = ...
BCNN(12, 30) = …
- Tìm thừa số phụ:
… : 12 = …
… : 30 = …
- Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng:
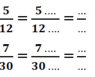
- Tìm BCNN( 12,30)
12 = 22.3
30 = 2 . 3 . 5
BCNN(12,30) = 22.3.5 = 60
- Tìm thừa số phụ:
60 : 12 = 5
60 : 30 = 2
- Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng;
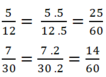
Đúng 0
Bình luận (0)
Tìm BCNN (306, 12)
Xem thêm câu trả lời
tìm BCNN (4 , 12)
tìm BCNN (4 , 12)
Tìm BCNN của: 10, 12, 15
10 = 2.5; 12 = 22.3; 15 = 3.5
⇒ BCNN(10, 12, 15) = 22.3.5 = 60.
Đúng 0
Bình luận (0)



















