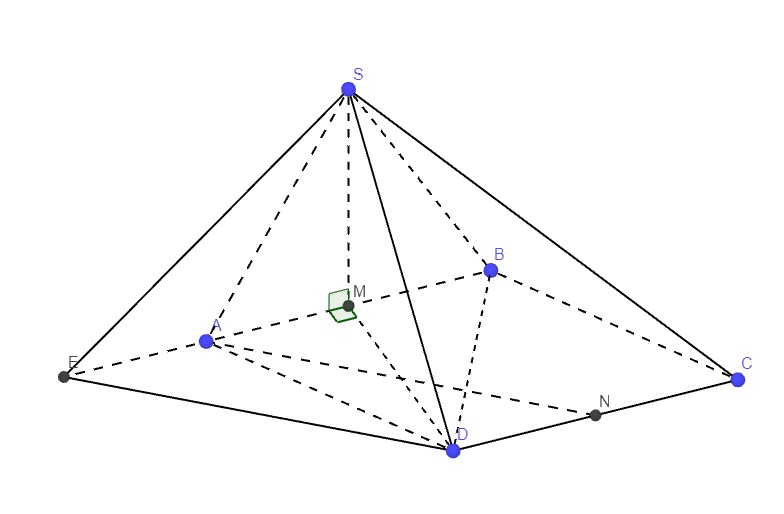
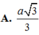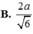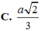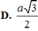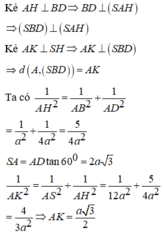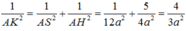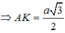cho hình chóp sabcd có đáy abcd là hình thoi, \(SD=a\sqrt{3}\), tất cả các cạnh bằng a. tính góc giữa 2đt SD và mp(ABCD)?

Những câu hỏi liên quan
Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = SD GỌI O LÀ tâm của hình thoi và SO =a√3/4 góc ABC bằng 60 độ a. Tính diện tích đáy ABCD b.tính thể tích hình chóp SABCD
a: Xét ΔBAC có BA=BC và góc ABC=60 độ
nên ΔABC đều
=>\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(S_{ABCD}=\dfrac{a^2\sqrt{3}}{2}\)
Đúng 0
Bình luận (0)
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với mp (ABCD), SD=a.căn 3. Gọi M và N lần lượt là hình chiếu của a lên SD và SB.
Tìm giao điểm K giữa SC và (AMN) và tính diện tích của MKNA
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với mp (ABCD), SD=a.căn 3. Gọi M và N lần lượt là hình chiếu của a lên SD và SB.
Tìm giao điểm K giữa SC và (AMN) và tính diện tích của MKNA
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a,
S
A
a
3
và vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng
A
B
C
D
bằng A.
60
°
B.
45
°
C.
30
°
D.
arcsin
3
5
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, S A = a 3 và vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng A B C D bằng
A. 60 °
B. 45 °
C. 30 °
D. arcsin 3 5
Đáp án A.
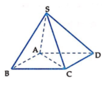
Ta có S A ⊥ ( A B C D ) nên A là hình chiếu của S trên mặt phẳng A B C D . Suy ra AD là hình chiếu của SD trên mặt phẳng A B C D .
Khi đó S D , A B C D ^ = S D , A D ^ = S D A ^ (do S D A ^ < 90 ° ).
Do Δ S A D vuông tại A nên tan S D A ^ = S A A D = a 3 a = 3 ⇒ S D A ^ = 60 ° .
Vậy S D , A B C D ^ = 60 ° .
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh bằng a, góc DAB bằng 60 độ, tam giác SAB đều và nằm trên mặt phẳng vuông góc với mặt đáy, gọi M, N là trung điểm của AB, CD tính cosin của góc giữa 2 đường thẳng AN và SD
Gọi E là điểm đối xứng M qua A
\(\Rightarrow ANDE\) là hình bình hành (cặp cạnh đối AE và DN song song và bằng nhau)
\(\Rightarrow AN||DE\Rightarrow\) góc giữa AN và SD bằng góc giữa SD và DE
Do tam giác ABD đều \(\Rightarrow MD\perp AB\) \(\Rightarrow\Delta MDE\) vuông tại M
Do tam giác SAB đều \(\Rightarrow SM\perp AB\)
Mà \(\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SM\perp\left(ABCD\right)\)
\(\Rightarrow\) Các tam giác SMD, SME vuông tại M
\(SM=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác SAB đều)
\(MD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác ABD đều)
\(ME=2AM=AB=a\)
Pitago:
\(SD=\sqrt{SM^2+MD^2}=\dfrac{a\sqrt{6}}{2}\)
\(SE=\sqrt{SM^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(ED=\sqrt{MD^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow cos\widehat{SDE}=\dfrac{SD^2+ED^2-SE^2}{2SD.ED}=\dfrac{\sqrt{42}}{14}\)
Đúng 1
Bình luận (0)
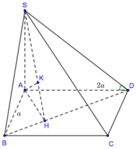
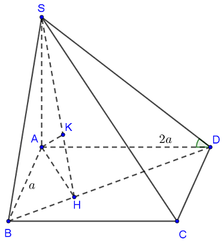
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,AC=a.Tam giác SAB cân và nằm trong mp vuông góc với đáy.Tính khoảng cách từ D đến (SBC).Biết góc giữa SD và mp đáy bằng 60.
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a tất cả các cạnh bên đều bằng a. Gọi điểmM thuộc SD sao cho SD =3SM, G là trọng tâm của tam giác BCD gọi (a) là mặt phẳng chứa MG và song song với CD. Xác định và tính diện tích thiết diện của hình chóp với mp (a)
Xem chi tiết
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng
A
B
C
D
. Biết
A
B
a
,
A
D
2
a
, góc giữa cạnh bên SD và mp
A
B
C
D
bằng
60
°
. Tính khoảng cách từ A đến mp...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng A B C D . Biết A B = a , A D = 2 a , góc giữa cạnh bên SD và mp A B C D bằng 60 ° . Tính khoảng cách từ A đến mp S B D .
A. a 3 3
B. 2 a 6
C. a 2 3
D. a 3 2
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng (ABCD). Biết AB a, AD 2a, góc giữa cạnh bên SD và mp (ABCD) bằng
60
°
. Tính khoảng cách từ A đến mp (SBD).
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng (ABCD). Biết AB = a, AD = 2a, góc giữa cạnh bên SD và mp (ABCD) bằng 60 ° . Tính khoảng cách từ A đến mp (SBD).