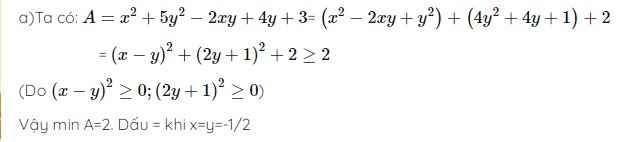a) \(2x^2-x+1=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)

\(ĐTXR\Leftrightarrow x=\dfrac{1}{4}\)

b) \(5x-x^2+4=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\)

\(ĐTXR\Leftrightarrow x=\dfrac{5}{2}\)

c) \(x^2+5y^2-2xy+4y+3=\left(x-y\right)^2+\left(2y+1\right)^2+2\ge2\)

\(ĐTXR\Leftrightarrow\)\(x=y=-\dfrac{1}{2}\)

b: ta có: \(-x^2+5x+4\)

\(=-\left(x^2-5x-4\right)\)

\(=-\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{41}{4}\right)\)

\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)

a: Ta có: \(A=x^2+3x+4\)

\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\)

\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\forall x\)

Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)

1:

a: =x^2-7x+49/4-5/4

=(x-7/2)^2-5/4>=-5/4

Dấu = xảy ra khi x=7/2

b: =x^2+x+1/4-13/4

=(x+1/2)^2-13/4>=-13/4

Dấu = xảy ra khi x=-1/2

e: =x^2-x+1/4+3/4=(x-1/2)^2+3/4>=3/4

Dấu = xảy ra khi x=1/2

f: x^2-4x+7

=x^2-4x+4+3

=(x-2)^2+3>=3

Dấu = xảy ra khi x=2

2:

a: A=2x^2+4x+9

=2x^2+4x+2+7

=2(x^2+2x+1)+7

=2(x+1)^2+7>=7

Dấu = xảy ra khi x=-1

b: x^2+2x+4

=x^2+2x+1+3

=(x+1)^2+3>=3

Dấu = xảy ra khi x=-1

a) Ta thấy: \(\left|\dfrac{2}{5}-x\right|\ge0\forall x\)

\(\Rightarrow Q=\dfrac{9}{2}+\left|\dfrac{2}{5}-x\right|\ge\dfrac{9}{2}\forall x\)

Dấu \("="\) xảy ra khi: \(\left|\dfrac{2}{5}-x\right|=0\Leftrightarrow\dfrac{2}{5}-x=0\Leftrightarrow x=\dfrac{2}{5}\)

Vậy \(Min_Q=\dfrac{9}{2}\) khi \(x=\dfrac{2}{5}\).

\(---\)

b) Ta thấy: \(\left|x+\dfrac{2}{3}\right|\ge0\forall x\)

\(\Rightarrow M=\left|x+\dfrac{2}{3}\right|-\dfrac{3}{5}\ge-\dfrac{3}{5}\forall x\)

Dấu \("="\) xảy ra khi: \(\left|x+\dfrac{2}{3}\right|=0\Leftrightarrow x+\dfrac{2}{3}=0\Leftrightarrow x=-\dfrac{2}{3}\)

Vậy \(Min_M=-\dfrac{3}{5}\) khi \(x=-\dfrac{2}{3}\).

\(---\)

c) Ta thấy: \(\left|\dfrac{7}{4}-x\right|\ge0\forall x\)

\(\Rightarrow-\left|\dfrac{7}{4}-x\right|\le0\forall x\)

\(\Rightarrow N=-\left|\dfrac{7}{4}-x\right|-8\le-8\forall x\)

Dấu \("="\) xảy ra khi: \(\left|\dfrac{7}{4}-x\right|=0\Leftrightarrow\dfrac{7}{4}-x=0\Leftrightarrow x=\dfrac{7}{4}\)

Vậy \(Max_N=-8\) khi \(x=\dfrac{7}{4}\).

a) Ta có: \(\left|\dfrac{2}{5}-x\right|\ge0\forall x\)

\(\Rightarrow Q=\dfrac{9}{2}+\left|\dfrac{2}{5}-x\right|\ge\dfrac{9}{2}\forall x\)

Dấu "=" xảy ra khi:

\(\dfrac{2}{5}-x=0\)

\(\Rightarrow x=\dfrac{2}{5}\)

Vậy: ... 

b) Ta có: \(\left|x+\dfrac{2}{3}\right|\ge0\forall x\)

\(\Rightarrow M=\left|x+\dfrac{2}{3}\right|-\dfrac{3}{5}\ge-\dfrac{3}{5}\)

Dấu "=" xảy ra:

\(x+\dfrac{2}{3}=0\)

\(\Rightarrow x=-\dfrac{2}{3}\)

Vậy: ...

c) Ta có: \(-\left|\dfrac{7}{4}-x\right|\le0\forall x\)

\(\Rightarrow N=-\left|\dfrac{7}{4}-x\right|-8\le-8\)

Dấu "=" xảy ra:

\(\dfrac{7}{4}-x=0\)

\(\Rightarrow x=\dfrac{7}{4}\)

Vậy: ...

`#\text{ID01}`

a)

`Q = 9/2 + |2/5 - x|`

Vì `|2/5 - x| \ge 0` `AA` `x`

`=> 9/2 + |2/5 - x| \ge 9/2` `AA` `x`

`=>` GTNN của Q là `9/2` khi `|2/5 - x| = 0`

`=> 2/5 - x = 0`

`=> x = 2/5`

b)

`M = |x + 2/3| - 3/5`

Vì `|x + 2/3| \ge 0` `AA` `x`

`=> |x + 2/3| - 3/5 \ge -3/5` `AA` `x`

`=>` GTNN của M là `-3/5` khi `|x + 2/3| = 0`

`=> x + 2/3 = 0`

`=> x = -2/3`

c)

`N=-|7/4 - x| - 8`

Vì `|7/4 - x| \ge 0` `AA` `x`

`=> -|7/4 - x| \le 0` `AA` `x`

`=> -|7/4 - x| - 8 \le -8` `AA` `x`

`=>` GTLN của N là `-8` khi `|7/4 - x| = 0`

`=> 7/4 - x = 0`

`=> x = 7/4`

B=y^2-y+1

=y^2-2*y*1/2+1/4+3/4

=(y-1/2)^2+3/4>=3/4

Dấu = xảy ra khi y=1/2

E=-x^2+x+2

=-(x^2-x-2)

=-(x^2-x+1/4-9/4)

=-(x-1/2)^2+9/4<=9/4

Dấu = xảy ra khi x=1/2

a) \(A=2\left|x-3\right|+\left|2x-10\right|=\left|2x-3\right|+\left|10-2x\right|\ge\left|2x-3+10-2x\right|=7\)

Dấu "=" xảy ra \(\Leftrightarrow\)\(\left(2x-3\right)\left(10-2x\right)\ge0\)\(\Leftrightarrow\)\(\frac{3}{2}\le x\le5\)

b) \(B\left|\frac{1}{4}x-8\right|+\left|2-\frac{1}{4}x\right|\ge\left|\frac{1}{4}x-8+2-\frac{1}{4}x\right|=6\)

Dấu "=" xảy ra \(\Leftrightarrow\)\(\left(\frac{1}{4}x-8\right)\left(2-\frac{1}{4}x\right)\ge0\)\(\Leftrightarrow\)\(8\le x\le32\)

a)

Ta có:

\(A=x^2-2x-1=x^2-2x+1-2=\left(x-1\right)^2-2\)

\(\ge0-2=-2\)

Vậy \(A_{min}=-2\), đạt được khi và chỉ khi \(x-1=0\Leftrightarrow x=1\)

b)\(B=4x^2+4x+8=4x^2+4x+1+7\)

\(=\left(2x+1\right)^2+7\ge0+7=7\)

Vậy \(B_{min}=7\), đạt được khi và chỉ khi \(2x+1=0\Leftrightarrow x=\dfrac{-1}{2}\)

c)

Ta có:

\(C=3x-x^2+2=2-\left(x^2-3x\right)\)

\(=2+\dfrac{9}{4}-\left(x^2-2x.\dfrac{3}{2}+\dfrac{9}{4}\right)\)

\(=\dfrac{17}{4}-\left(x-\dfrac{3}{2}\right)^2\le\dfrac{17}{4}-0=\dfrac{17}{4}\)

Vậy \(C_{max}=\dfrac{17}{4}\), đạt được khi và chỉ khi \(x-\dfrac{3}{2}=0\Leftrightarrow x=\dfrac{3}{2}\)

d) Ta có:

\(D=-x^2-5x=-\left(x^2+5x\right)=\dfrac{25}{4}-\left(x^2+2x.\dfrac{5}{2}+\dfrac{25}{4}\right)\)

\(=\dfrac{25}{4}-\left(x+\dfrac{5}{2}\right)^2\le\dfrac{25}{4}-0=\dfrac{25}{4}\)

Vậy \(D_{max}=\dfrac{25}{4}\), đạt được khi và chỉ khi \(x+\dfrac{5}{2}=0\Leftrightarrow x=-\dfrac{5}{2}\)

e) Ta có:

\(E=x^2-4xy+5y^2+10x-22y+28\)

\(=x^2+4y^2+5^2-4xy+10x-20y+y^2-2y+1+2\)

\(=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\)

\(\ge0+0+2=2\)

Vậy \(E_{min}=2\), đạt được khi và chỉ khi \(x-2y+5=y-1=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)

\(a,-x^2+2x+5=-\left(x^2-2x-5\right)=-\left(x^2-2x+1-6\right)=-\left(x-1\right)^2+6\le6\)

dấu'=' xảy ra<=>x=1=>Max A=6

\(b,B=-x^2-y^2+4x+4y+2=-x^2+4x-4-y^2+4x-4+10\)

\(=-\left(x^2-4x+4\right)-\left(y^2-4x+4\right)+10\)

\(=-\left(x-2\right)^2-\left(y-2\right)^2+10=-\left[\left(x-2\right)^2+\left(y-2\right)^2\right]+10\le10\)

dấu"=" xảy ra<=>x=y=2=>Max B=10

\(c,C=x^2+y^2-2x+6y+12=\left(x-1\right)^2+\left(y+3\right)^2+2\ge2\)

dấu'=' xảy ra<=>x=1,y=-3=>MinC=2