Cho đường tròn tâm O, bán kính OA bằng 10dm. Tính độ dài đường kính AB.
Những câu hỏi liên quan
SGK Toán 3 tập 2 - Bộ sách Cánh diều - Trang 25
28 tháng 3 2023 lúc 18:24
a) Cho hình tròn tâm O có độ dài đường kính bằng 8 cm. Tính độ dài bán kính của hình tròn đó.
b) Cho hình tròn tâm O có độ dài bán kính bằng 5 cm. Tính độ dài đường kính của hình tròn đó.
`a,` Bán kính hình tròn là :
`8 : 2=4(cm)`
b,` Đường kính hình tròn là :
`5 xx 2=10(cm)`
Đúng 2
Bình luận (0)
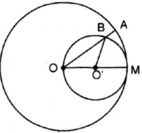
Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm O', đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
Chứng minh M A ⏜ và M B ⏜ có độ dài bằng nhau.
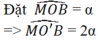(góc nội tiếp và góc ở tâ của đường tròn (O'))
Độ dài cung M A ⏜ là:
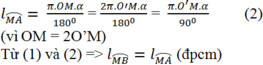
Đúng 0
Bình luận (0)
Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm O', đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
Chứng minh cung Ma và cung MB có độ dài bằng nhau
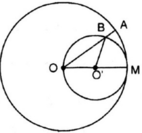
Kiến thức áp dụng
+ Trên đường tròn đường kính R, độ dài cung n0 bằng :
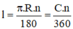
Đúng 0
Bình luận (0)
Cho một điểm M thuộc đường tròn tâm O đường kính R. Vẽ đường tròn tâm O' bán kính r có đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
a) Chứng minh cung MA và cung MB có độ dài bằng nhau.
b) Biết góc AOM = 45 độ và R = 10cm. Tính diện tích giới hạn bởi cung MA, cung MB và đoạn AB.
Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm O', đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B. Chứng minh cung MA và cung MB có độ dài bằng nhau.
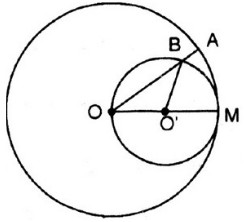
Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB
Đúng 0
Bình luận (0)
Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB
Đúng 0
Bình luận (0)
Cho một điểm M thuộc đường tròn tâm O đường kính R. Vẽ đường tròn tâm O' bán kính r có đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
a) Chứng minh cung MA và cung MB có độ dài bằng nhau.
b) Biết góc AOM = 450 và R = 10cm. Tính diện tích giới hạn bởi cung MA, cung MB và đoạn AB.
Vẽ đường tròn (O;2cm). Gọi A là một điểm nằm ngoài đường tròn (O;2cm). OA cắt đường tròn (O;2cm) ở B biết OA= 3 cm.
a) Tính AB
b) vẽ đường tròn tâm B bán kính BA. Hỏi điểm O có nằm trong đường tròn tâm B bán kính AB không? Vì sao?
c) đường tròn tâm B bán kính BA cắt đường tròn tâm O bán kính 2cm ở P và Q, cắt OA ở K. Chứng tỏ K nằm trong đường tròn tâm O bán kính 2 cm
cho hình tròn tâm O bán kính OA=2cm,đường kính MN
đúng ghi Đ,sai ghi S vào ô trống:
A.đường kính MN có độ dài bằng 20 mm ..........
B. đường kính MN có độ dài bằng 4 cm ..........
C. độ dài đoạn OA bằng 1/2 độ dài đoạn MN..........
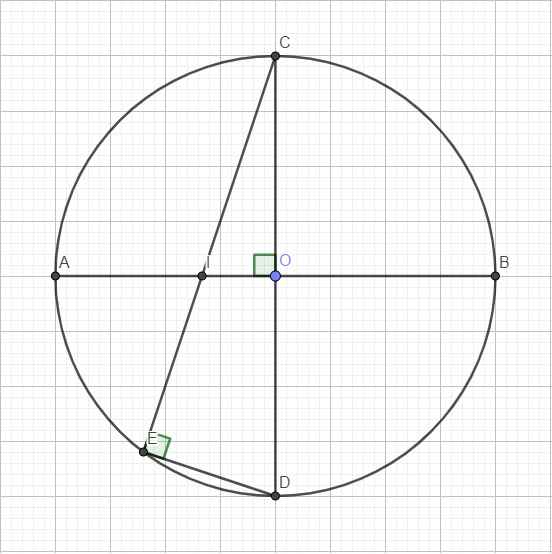
Cho đường tròn tâm O bán kính R, có hai đường kính AB và CD vuông góc với nhau.
Trên bán kính OA lấy điểm I sao cho AI=2/3 R
. Tia CI cắt đường tròn (O) tại điểm thứ hai E.
a) Chứng minh tam giác COI và tam giác CED đồng dạng
b) Tính độ dài dây CE.
b.
Áp dụng định lý Pitago trong tam giác vuông COI:
\(CI=\sqrt{OC^2+OI^2}=\sqrt{R^2+\left(\dfrac{R}{3}\right)^2}=\dfrac{R\sqrt{10}}{3}\)
Do 2 tam giác COI và CED đồng dạng
\(\Rightarrow\dfrac{CE}{CO}=\dfrac{CD}{CI}\Rightarrow CE=\dfrac{CD.CO}{CI}=\dfrac{2R.R}{\dfrac{R\sqrt{10}}{3}}=\dfrac{3R\sqrt{10}}{5}\)
Đúng 2
Bình luận (0)
a: Xét (O) có
ΔCED nội tiếp đường tròn
CD là đường kính
Do đó: ΔCED vuông tại E
Xét ΔCOI vuông tại O và ΔCED vuông tại E có
\(\widehat{ICO}\) chung
Do đó: ΔCOI\(\sim\)ΔCED
Đúng 2
Bình luận (0)