cho tam giác abc m thuộc ab n thuộc ac, biết AM/AB = MN/BC. Chứng minh MN//BC
Những câu hỏi liên quan
cho tam giác ABC (AB<AC).Trên cạnh AB lấy điểm M,từ mker MN//BC (M thuộc AC)
a, Chứng minh AB/AC=MN?BC
b, tìm MN biết AB=5,AM=2,BC=8
a: Sửa đề: \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
Xét ΔAMN và ΔABC có
\(\widehat{AMN}=\widehat{ABC}\)(hai góc đồng vị, MN//BC)
\(\widehat{A}\) chung
Do đó: ΔAMN đồng dạng với ΔABC
=>\(\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
b: \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)
=>\(\dfrac{MN}{8}=\dfrac{2}{5}\)
=>\(MN=2\cdot\dfrac{8}{5}=\dfrac{16}{5}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn. Vẽ phân giác AD (D thuộc BC), Vẽ DM//AB ( M thuộc AC)
a. Chứng minh tam giác MAD cân tại M
b. Vẽ MN//BC (N thuộc AB). Chứng minh tam giác MND= tam giác BDN
c. Chứng minh AM=BN
a: Ta có: \(\widehat{MAD}=\widehat{BAD}\)(AD là tia phân giác của góc BAC)
\(\widehat{BAD}=\widehat{MDA}\)(hai góc so le trong, AB//DM)
Do đó: \(\widehat{MAD}=\widehat{MDA}\)
=>ΔMAD cân tại M
b: Xét ΔMND và ΔBDN có
\(\widehat{MND}=\widehat{BDN}\)(hai góc so le trong, NM//BD)
ND chung
\(\widehat{MDN}=\widehat{BND}\)(hai góc so le trong, MD//BN)
Do đó: ΔMND=ΔBDN
c: Ta có: ΔMND=ΔBDN
=>MD=BN
mà MD=MA
nên MA=BN
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 4cm, AC = 6cm. Lấy M thuộc AB sao cho AM = 2cm. Lấy N thuộc AC sao cho AN = 3cm. Chứng minh MN // BC.
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
Đúng 0
Bình luận (0)
a, Cho tam giác ABC. M thuộc AB ,N thuộc AC sao cho MN//BC .Biết AM=3cm;AB=4cm ;AN=2cm ;BC=6cm .Tính NC ,MN?
Cho tam giác ABC nhọn, AB=6cm, BC=8cm.Gọi M,N theo thứ tự là trung điểm của AB và BC.
a, Chứng minh MN//AC
b, Chứng minh AM×BC=AB×BN
c,Kẻ phân giác BP(P thuộc AC) chứng minh rằng AM/CN=PA/PC
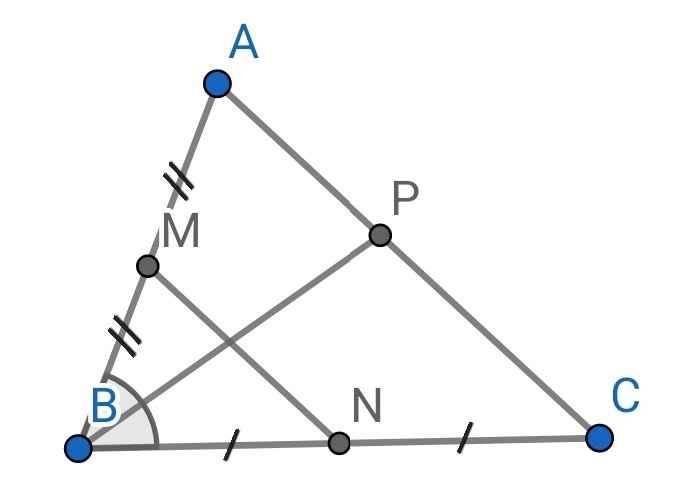a) Do M là trung điểm của AB (gt)
⇒ AM = BM = AB : 2 = 6 : 2 = 3 (cm)
Do N là trung điểm của BC (gt)
⇒ BN = CN = BC : 2 = 8 : 2 = 4 (cm)
Ta có:
BM/AM = 3/3 = 1
BN/CN = 4/4 = 1
⇒ BM/AM = BN/CN
⇒ MN // AC (định lý Ta-lét)
b) Ta có:
AM.BC = 3.8 = 24 (cm)
AB.BN = 6.4 = 24 (cm)
⇒ AM.BC = AB.BN
c) Do BP là tia phân giác của ∠ABC (gt)
⇒ BA/BC = PA/PC (1)
Do MN // AC (cmt)
⇒ BA/BC = AM/CN (2)
Từ (1) và (2) ⇒ AM/CN = PA/PC
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn, AB=6cm, BC=8cm.Gọi M,N theo thứ tự là trung điểm của AB và BC a, Chứng minh MN//AC b, Chứng minh AM×BC=AB×BN c,Kẻ phân giác BP(P thuộc AC) chứng minh rằng AM/CN=PA/PC
cho tam giác ABC cân tại A lấy dđiểm M thuộc cạnh AB điểm N thuộc AC sao cho AM=AN chứng minh MN//BC
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
Đúng 2
Bình luận (0)
\(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ACB}=\dfrac{180^o-\widehat{BAC}}{2}\) ( 1)
Mặt khác , ta có AM = AN \(\Rightarrow\Delta AMN\) cân tại A
\(\Rightarrow\widehat{ANM}=\dfrac{180^o-\widehat{MAN}}{2}\) ( mà \(M\in AB;N\in AC\) nên \(\widehat{MAN}=\widehat{BAC}\) )
\(\Rightarrow\widehat{ANM}=\dfrac{180^o-\widehat{BAC}}{2}\) ( 2 )
Từ (1), (2)\(\Rightarrow\) \(\widehat{ACB}=\widehat{ANM}\) mà 2 góc này ở vị trí so le trong tại MN và BC nên MN // BC ( đpcm)
( Giải thích (1) : \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^O\) \(\Rightarrow\widehat{ABC}+\widehat{ACB}=180^O-\widehat{BAC}\) mà \(\widehat{ABC}=\widehat{ACB}\) do \(\Delta ABC\) cân tại A
\(\Rightarrow2.\widehat{ACB}=180^O-\widehat{BAC}\)
\(\Rightarrow\widehat{ACB}=\dfrac{180^O-\widehat{BAC}}{2}\)
Còn (2) thì tương tự như (1) )
Đúng 0
Bình luận (0)
Cho tam giác ABC ,trên cạnh AB và AC lần lượt lấy hai điểm M và N. Biết AM=3cm, BM=2cm, AN=7,5cm , NC=5cm. a) chứng minh rằng MN//BC b) đường trung tuyến AI ( I thuộc BC) của tam giác ABC cắt MN tại K. Chứng minh K là trung điểm của MN
cho tam giác ABC vuông tại A, Có góc ABC 60^0. Vẽ AHperpBC (H thuộc BC ).Phân giác của góc HAC cắt BC tại M. MNperpAC (N thuộc AC)a) giả sử AB3cm, BC5cm. Tính cạnh AC b) chứng minh AM là đường trung trực của HNc) chứng minh tam giác AHN là một tam giác đềud) đường thẳng HN cắt AB ở D. chứng minh H là trung điểm của ND
Đọc tiếp
cho tam giác ABC vuông tại A, Có góc ABC = \(60^0\). Vẽ AH\(\perp\)BC (H thuộc BC ).
Phân giác của góc HAC cắt BC tại M. MN\(\perp\)AC (N thuộc AC)
a) giả sử AB=3cm, BC=5cm. Tính cạnh AC
b) chứng minh AM là đường trung trực của HN
c) chứng minh tam giác AHN là một tam giác đều
d) đường thẳng HN cắt AB ở D. chứng minh H là trung điểm của ND
a: AC=4cm
b: Xét ΔAMH vuông tại H và ΔAMN vuông tại N có
AM chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔAMN
Suy ra: MH=MN; AH=AN
hay AM là đường trung trực của NH
c: Xét ΔAHN có AH=AN
nên ΔAHN cân tại A
mà \(\widehat{HAN}=60^0\)
nên ΔAHN đều
Đúng 1
Bình luận (0)