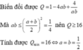\(a)\) Ta có : 

\(M=a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)\)

Thay \(a+b=1\) vào \(M=\left(a+b\right)\left(a^2+b^2-ab\right)\) ta được : 

\(M=\left(a+b\right)\left(a^2+b^2-ab\right)=1\left(a^2+b^2-ab\right)=a^2+b^2-ab\)

Lại có : 

\(a^2\ge0\)

\(b^2\ge0\)

\(\Rightarrow\)\(a^2+b^2\ge0\)

\(\Rightarrow\)\(a^2+b^2-ab\ge-ab\)

Dấu "=" xảy ra khi \(\hept{\begin{cases}a^2=0\\b^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=0\\b=0\end{cases}}}\)

Vậy \(M_{min}=-ab\) khi \(a=b=0\)

Sai thì thôi nhé, mk mới lớp 7 

dytt me dễ vãi lone

\(a^3+\frac{1}{8}+\frac{1}{8}\ge3\sqrt[3]{\frac{a^3.1}{8.8}}=\frac{3}{4}a.\)

\(b^3+\frac{1}{8}+\frac{1}{8}\ge\frac{3}{4}b\)

\(M+\frac{4}{8}\ge\frac{3}{4}\left(a+b\right)=\frac{3}{4}\Leftrightarrow M\ge\frac{3}{4}-\frac{4}{8}=?\) tự tính dcmmm

b.

\(a^3+1+1\ge3\sqrt[3]{a^3}=3a\)

\(b^3+1+1\ge3b\)

\(a^3+b^3+4\ge3\left(A+b\right)\)

cái dmcmmm a^3+b^3=2 suy ra

\(6\ge3\left(a+b\right)\)

\(2\ge a+b\)

dytt cụ m tự kết luận

\(5,M=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\\ M=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]\\ M=1\left(1-3ab\right)=1-3ab\ge1-\dfrac{3\left(a+b\right)^2}{4}=1-\dfrac{3}{4}=\dfrac{1}{4}\\ M_{min}=\dfrac{1}{4}\Leftrightarrow a=b=\dfrac{1}{2}\)

Câu 5:

\(a+b=1\Rightarrow a=1-b\)

\(M=a^3+b^3=\left(1-b\right)^3+b^3=1-3b+3b^2-b^3+b^3\)

\(=1-3b+3b^2=3\left(b^2-b+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(b-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)

\(minM=\dfrac{1}{4}\Leftrightarrow a=b=\dfrac{1}{2}\)

Câu 7:

\(a^3+b^3+abc\ge ab\left(a+b+c\right)\)

\(\Leftrightarrow a^3+b^3+abc-ab\left(a+b+c\right)\ge0\)

\(\Leftrightarrow a^3+b^3-a^2b-ab^2\ge0\)

\(\Leftrightarrow a^2\left(a-b\right)-b^2\left(a-b\right)\ge0\)

\(\Leftrightarrow\left(a-b\right)\left(a^2-b^2\right)\ge0\Leftrightarrow\left(a-b\right)^2\left(a+b\right)\ge0\)(đúng do a,b dương)

Dấu "=" xảy ra \(\Leftrightarrow a=b\)

giúp mình vs

5.

Với mọi a;b ta có: \(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2\ge2ab\Rightarrow2a^2+2b^2\ge a^2+b^2+2ab\)

\(\Rightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\Rightarrow a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2=\dfrac{1}{2}\)

\(M=a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)=a^2+b^2-ab\)

\(M=\dfrac{3}{2}\left(a^2+b^2\right)-\dfrac{1}{2}\left(a+b\right)^2=\dfrac{3}{2}\left(a^2+b^2\right)-\dfrac{1}{2}\ge\dfrac{3}{2}.\dfrac{1}{2}-\dfrac{1}{2}=\dfrac{1}{4}\)

\(M_{min}=\dfrac{1}{4}\) khi \(a=b=\dfrac{1}{2}\)

6.

Do \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=2>0\)

Mà \(a^2-ab+b^2>0\Rightarrow a+b>0\)

Mặt khác với mọi a;b ta có:

\(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2\ge2ab\Rightarrow a^2+b^2+2ab\ge4ab\)

\(\Rightarrow\left(a+b\right)^2\ge4ab\Rightarrow ab\le\dfrac{1}{4}\left(a+b\right)^2\) \(\Rightarrow-ab\ge-\dfrac{1}{4}\left(a+b\right)^2\)

Từ đó:

\(2=a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\ge\left(a+b\right)^3-3.\dfrac{1}{4}\left(a+b\right)^2\left(a+b\right)=\dfrac{1}{4}\left(a+b\right)^3\)

\(\Rightarrow\left(a+b\right)^3\le8\Rightarrow a+b\le2\)

\(N_{max}=2\) khi \(a=b=1\)

7.

Ta có:

\(a^3+b^3+abc=\left(a+b\right)\left(a^2+b^2-ab\right)+abc\ge\left(a+b\right)\left(2ab-ab\right)+abc\)

\(\Rightarrow a^3+b^3+abc\ge ab\left(a+b\right)+abc=ab\left(a+b+c\right)\) (đpcm)

Dấu "=" xảy ra khi \(a=b\)

8.

\(\left|a+b\right|>\left|a-b\right|\Leftrightarrow\left(a+b\right)^2>\left(a-b\right)^2\)

\(\Leftrightarrow a^2+2ab+b^2>a^2-2ab+b^2\)

\(\Leftrightarrow4ab>0\Leftrightarrow ab>0\)

\(\Rightarrow a;b\) cùng dấu

Ta có : a3+b3=(a+b)3−3ab(a+b)=1−3ab

Vì a+b=1a+b=1  là một tổng không đổi nên ab đạt giá trị lớn nhất khi a = b

=> -ab đạt giá trị nhỏ nhất khi a = b mà a + b = 1 => a = b = 1/2

Thay a = b = 1/2 vào M được a3+b3≥(12)3+(12)3=14a3+b3≥(12)3+(12)3=14

Vậy min M = 1/4 <=> a = b = 1/2

Ta có: M = a3 + b3 = ( a + b ) * 3 = 1 * 3 = 3

\(a+b=1\Leftrightarrow a=1-b\\ M=a^3+b^3=a^3+\left(1-a\right)^3\\ =a^3+1-3a+3a^2-a^3\\ =3a^2-3a+1=3\left(a^2-a+\dfrac{1}{4}+\dfrac{1}{12}\right)=3\left(a-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)

Dấu \("="\Leftrightarrow a=b=\dfrac{1}{2}\)

\(F=\left(a+b\right)^3-3ab\left(a+b\right)+ab=1-2ab\)

Ta có F đạt giá trị nhỏ nhất khi -2ab đạt giá trị nhỏ nhất.

Vì \(a+b=1\) có tổng không đổi nên \(-2ab\) đạt giá trị

nhỏ nhất khi ab đạt giá trị lớn nhất <=> a = b = 1/2

Thay a = b = 1/2 vào F tính được min F.

Ta có : F = (a+b)(a2 –ab+b2) +ab

Thay a+ b =1 vào F ta được F = a2 – ab +b2 + ab

F = a2 +b2 F = (a+b)2 – 2ab
F = 1 – 2ab Do a+b =1 ⇔ a = 1-b

thay vào F ta có : F = 1- 2(1-b)b F = 1 -2b+2b2 F = 2(b2 – b+41) + 21 F = 2(b -21)2 +21≥21

Với mọi b Dấu “ = ” xảy ra khi : b -21 = 0 ⇔ b =21 và a =21 Vậy Min F = 21 Khi a =b = 21