Tìm số tự nhiên n để đa thức:
A(x)=x2n+xn+1 chia hết cho đa thức x2+x+1.
Tìm số tự nhiên n để đa thức:
A(x)=x2n+xn+1 chia hết cho đa thức x2+x+1.
Vì \(A\left(x\right)=x^{2n}+x^n+1\) chỉ có một hằng số là1
đa thức \(x^2+x+1\) cũng chỉ có một hằng số là 1
Để \(A\left(x\right)⋮x^2+x+1\) thì thì \(A\left(x\right)\) phải có số mũ tương ứng với các bậc như đa thức : => n=1
-Đáp án cuối cùng: \(n=3k+1\) hay \(n=3k+2\)



Cho đa thức A(x) = 1 + x2 + x4 + .... + x2n - 2; B= 1 + x + x2 + ... + xn-1. Tìm số nguyên dương n để đa thức A(x) chia hết cho đa thức B(x).
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
a)tìm giá trị nhỏ nhất của biểu thức:A=x2-4xy+5y2+10x-22y+28
b)tìm n để đa thức 3x3+10x2-5+n chia hết cho đa thức 3x+1
c)tìm tất cả các số nguyên n để 2n2+n-7 chia hết cho n-2
\(a,A=\left(x^2-4xy+4y^2\right)+10\left(x-2y\right)+25+\left(y^2-2y+1\right)+2\\ A=\left(x-2y\right)^2+10\left(x-2y\right)+5+\left(y-1\right)^2+2\\ A=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=2y-5\\y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)
\(b,\Leftrightarrow3x^3+10x^2-5+n=\left(3x+1\right)\cdot a\left(x\right)\)
Thay \(x=-\dfrac{1}{3}\Leftrightarrow3\left(-\dfrac{1}{27}\right)+10\cdot\dfrac{1}{9}-5+n=0\)
\(\Leftrightarrow-\dfrac{1}{9}+\dfrac{10}{9}-5+n=0\\ \Leftrightarrow-4+n=0\Leftrightarrow n=4\)
\(c,\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\\ \Leftrightarrow2n\left(n-2\right)+5\left(n-2\right)+3⋮n-2\\ \Leftrightarrow n-2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow n\in\left\{-1;1;3;5\right\}\)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
a: \(\Leftrightarrow2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x+2+a-2⋮x^2-x+1\)
=>a=2
Bai 1:
a)Tìm n để đa thức x^4-x^3+6x^2-x+n chia hết cho đa thức x^2-x+5
b)Tìm n để đa thức 3x^3+10x^2-5+n chia hết cho đa thức 3x+1
c)Tìm tất cả các số nguyên n để 2n^2+n-7 chia hết cho n-2
ĐỂ x4 - x3 + 6x2 -x \(⋮x^2-x+5\)
\(\Rightarrow x-5=0\Rightarrow x=5\)
b , ta có : \(3x^3+10x^2-5⋮3x+1\)
\(\Rightarrow3x^3+x^2+9x^2+3x-3x-1-4⋮3x+1\)
\(\Rightarrow x\left(3x+1\right)+3x\left(3x+1\right)-\left(3x+1\right)-4⋮3x+1\)
mà : \(\left(3x+1\right)\left(4x-1\right)⋮3x+1\)
\(\Rightarrow4⋮3x+1\Rightarrow3x+1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Nếu : 3x + 1 = 1 => x = 0 ( TM )
3x + 1 = -1 => x = -2/3 ( loại )
3x + 1 = 2 => x = 1/3 ( loại )
3x + 1 = -2 => x = -1 ( TM )
3x + 1 = 4 => x = 1 ( TM )
3x + 1 = -1 => x = -5/3 ( loại )
\(\Rightarrow x\in\left\{0;\pm1\right\}\)
kiều hoa câu b dòng thứ 3 phải là\(x^2\left(3x+1\right)\)chứ
Tìm số tự nhiên n để đa thức A chia hết cho đa thức B khi A=x^2.y^4 +2x^3.y^3 và B=x^n.y^3
Ta có: \(A=x^2y^4+2x^3y^3\)
Để A chia hết cho \(B=x^ny^3\) thì:
\(\left\{{}\begin{matrix}2x^3y^3⋮x^ny^3\\x^2y^4⋮x^ny^3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^3⋮x^n\\x^2⋮x^n\end{matrix}\right.\)
\(\Rightarrow x^0\le x^n\le x^2\)
\(\Rightarrow0\le n\le2\)
Tìm a, b để đa thức A ( x ) = 2 x 3 – x 2 + a x + b chia hết cho đa thức B ( x ) = x 2 – 1
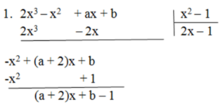
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0
Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1