
giúp em bài hình với ạ
Ai giúp em bài hàm số với bài hình với ạ nếu rảnh giúp em luôn câu c, bài rút gọn ạ;v

Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)
Giúp em bài 6 với 9 với ạ. Vẽ hình giúp en nx. Em cảm ơn ạ. 
Bài 10:
a: \(\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OA}\)
\(=\overrightarrow{AO}+\overrightarrow{OA}=\overrightarrow{0}\)
b: \(\overrightarrow{OA}+\overrightarrow{BC}+\overrightarrow{DO}+\overrightarrow{CD}\)
\(=\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{BD}\)
\(=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BA}\)
 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2
giúp em bài 1 với ạ ko cần hình vẽ ,em cần gấp lắm ạ

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
hay MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành
giúp em 7 bài này với ạ em cần gấpp!! ( vẽ cả hình đk ạ)
( Hình em tự vẽ nhé )
+ Ta có: ΔABC = ΔDEF
=> \(\widehat{A}=\widehat{D}=30^o\)
+ Ta có: \(2\widehat{B}=3\widehat{C}\)
=> \(\widehat{B}=\dfrac{3\widehat{C}}{2}\)
+ Xét ΔABC
=> \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(t3g\Delta\right)\)
Mà \(\widehat{A}=30^o;\widehat{B}=\dfrac{3\widehat{C}}{2}\)
=> \(30^o+\dfrac{3\widehat{C}}{2}+\widehat{C}=180^o\)
=> \(\dfrac{3\widehat{C}}{2}+\widehat{C}=150^o\)
\(\Rightarrow\dfrac{3\widehat{C}}{2}+\dfrac{2\widehat{C}}{2}=150^o\)
\(\Rightarrow\dfrac{5\widehat{C}}{2}=150^o\)
\(\Rightarrow5\widehat{C}=75^o\)
\(\Rightarrow\widehat{C}=15^o\)
+ Xét ΔABC
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(t3g\Delta\right)\)
\(\Rightarrow30^o+15^o+\widehat{B}=180^o\)
\(\Rightarrow\widehat{B}=135^o\)
Giúp em viết một bài cách làm xôi gấc bằng tiếng anh với ạ , cách trình bằng như hình bên dưới . Giúp em với ạ , em đang cần gấp 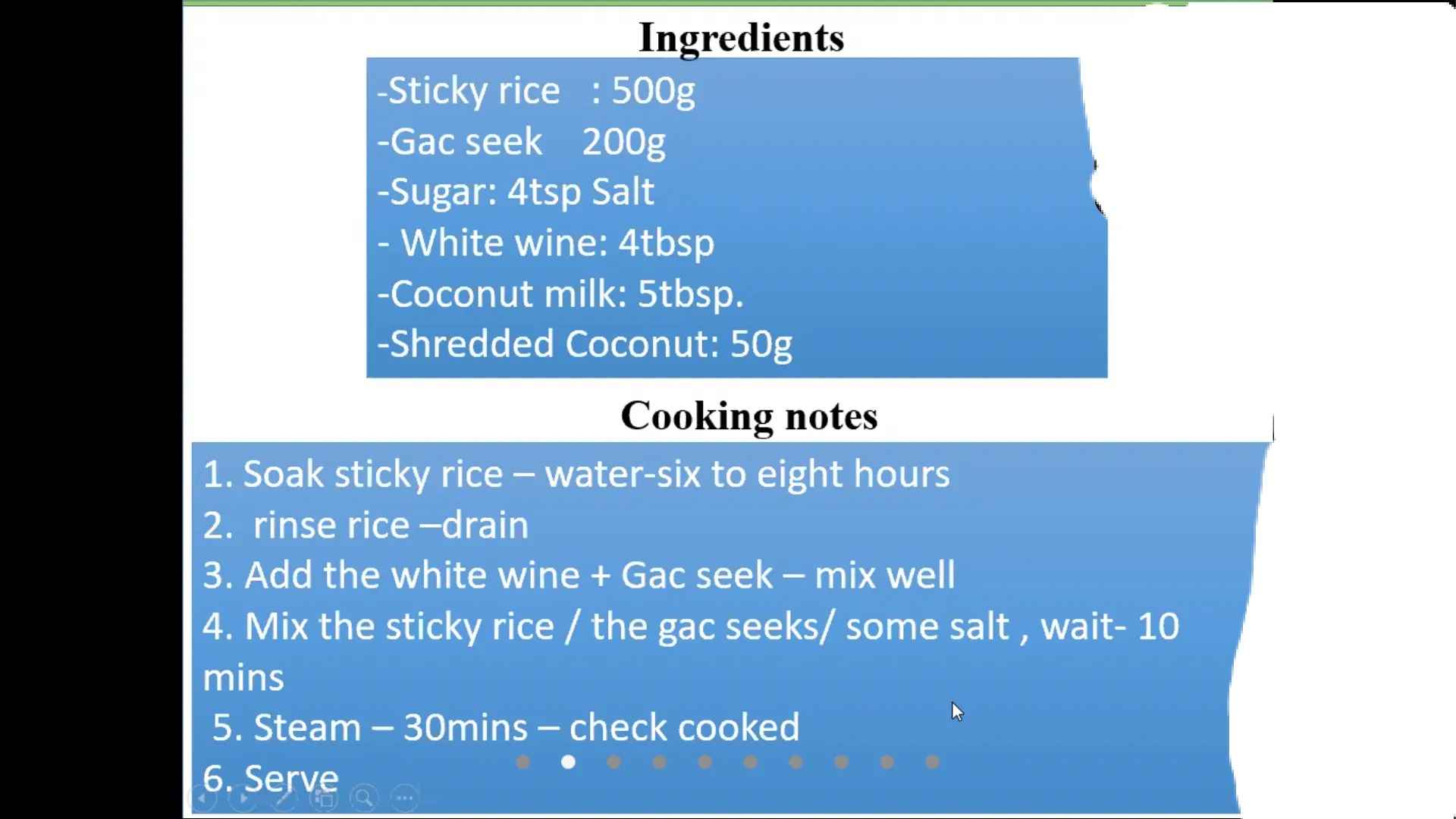
Bài hình học ạ giúp em với
Giúp em bài hình này với ạ 
a)Ta có:
`hat{BFC}` là góc chẵn nửa (O)
`=>hat{BFC}=90^o`
Tương tự:`hat{BEC}=90^o`
Xét tam giác ABC có:
`CFbotAB(CMT)`
`AEbotAC(CMT)`
Mà CF cắt BE tại H
`=>H` là trực tâm tam giác ABC
`=>AHbotBC`
Hay `AD bot BC`
Vì `hat{BFH}=hat{BDH}=90^o`
`=>hat{BFH}+hat{BDH}=180^o`
`=>` tg BFHD nt
`=>hat{DFC}=hat{DBE}`
b)Vì `hat{EBC}=hat{EFC}`(cùng chắn cung EC nhỏ)
Mà tg BFHD nt
`=>hat{DFH}=\hat{HBD}`
`=>hat{DFH}=hat{EFC}`
`=>` FC là pg `hat{EFD}`
Vì `FC` là pg `hat{EFD}`
`=>hat{EFD}=2hat{DFH}`
Mà `hat{DFH}=hat{HBD}`
`=>hat{EFD}=2hat{DBH}`
Mà `hat{EOC}=2hat{DBH}`(góc nội tiếp và góc ở tâm)
`=>hat{EFD}=hat{EOC}`
`=>` tg OEFD nt (do trong = góc ngoài tại đỉnh đối)
Giúp em câu 2 bài hình với ạ. Em cảm ơn
a.
Qua S kẻ đường thẳng d song song AB
Do \(\left\{{}\begin{matrix}AB\in\left(SAB\right)\\CD\in\left(SCD\right)\\AB||CD\\S\in\left(SAB\right)\cap\left(SCD\right)\end{matrix}\right.\)
\(\Rightarrow d=\left(SAB\right)\cap\left(SCD\right)\)
b.
Gọi E là trung điểm AD, kéo dài AG cắt SD tại F \(\Rightarrow F\) là trung điểm SD (do G là trọng tâm SAD)
AM thuộc AB nên AM cắt SB tại B \(\Rightarrow B'\) trùng B
Trong mp (SCD), qua F kẻ đường thẳng song song CD cắt SC tại C'
\(\Rightarrow C'\) là trung điểm SC (do F là trung điểm SD)
Trong mp (ABCD), kéo dài AB và CE cắt nhau tại H
3 mp (SCE), (ABCD), (AGM) cắt nhau theo 3 giao tuyến phân biệt AB, CE, C'G, mà AB và CE cắt nhau tại H \(\Rightarrow\) 3 đường thẳng đồng quy tại H (theo t/c giao tuyến 3 mp cắt nhau)
Hay C',G,H thẳng hàng
\(AE||CB\) ; \(AE=\dfrac{1}{2}AD=\dfrac{1}{2}CB\Rightarrow\) AE là đường trung bình tam giác HCB
\(\Rightarrow A\) là trung điểm BH và E là trung điểm CH
\(\Rightarrow G\) là trọng tâm tam giác SCH
\(\Rightarrow\dfrac{HG}{HC'}=\dfrac{2}{3}\) (1)
Theo giả thiết \(MB=2MA\Rightarrow AB-MA=2MA\Rightarrow MA=\dfrac{1}{3}AB=\dfrac{1}{3}AH\)
\(\Rightarrow\dfrac{HM}{BH}=\dfrac{AH+AM}{2AH}=\dfrac{AH+\dfrac{1}{3}AH}{2AH}=\dfrac{2}{3}\) (2)
(1);(2) \(\Rightarrow\dfrac{HG}{HC'}=\dfrac{HM}{BH}\Rightarrow MG||BC'\)
Hay \(MG||B'C'\) (do B trùng B')