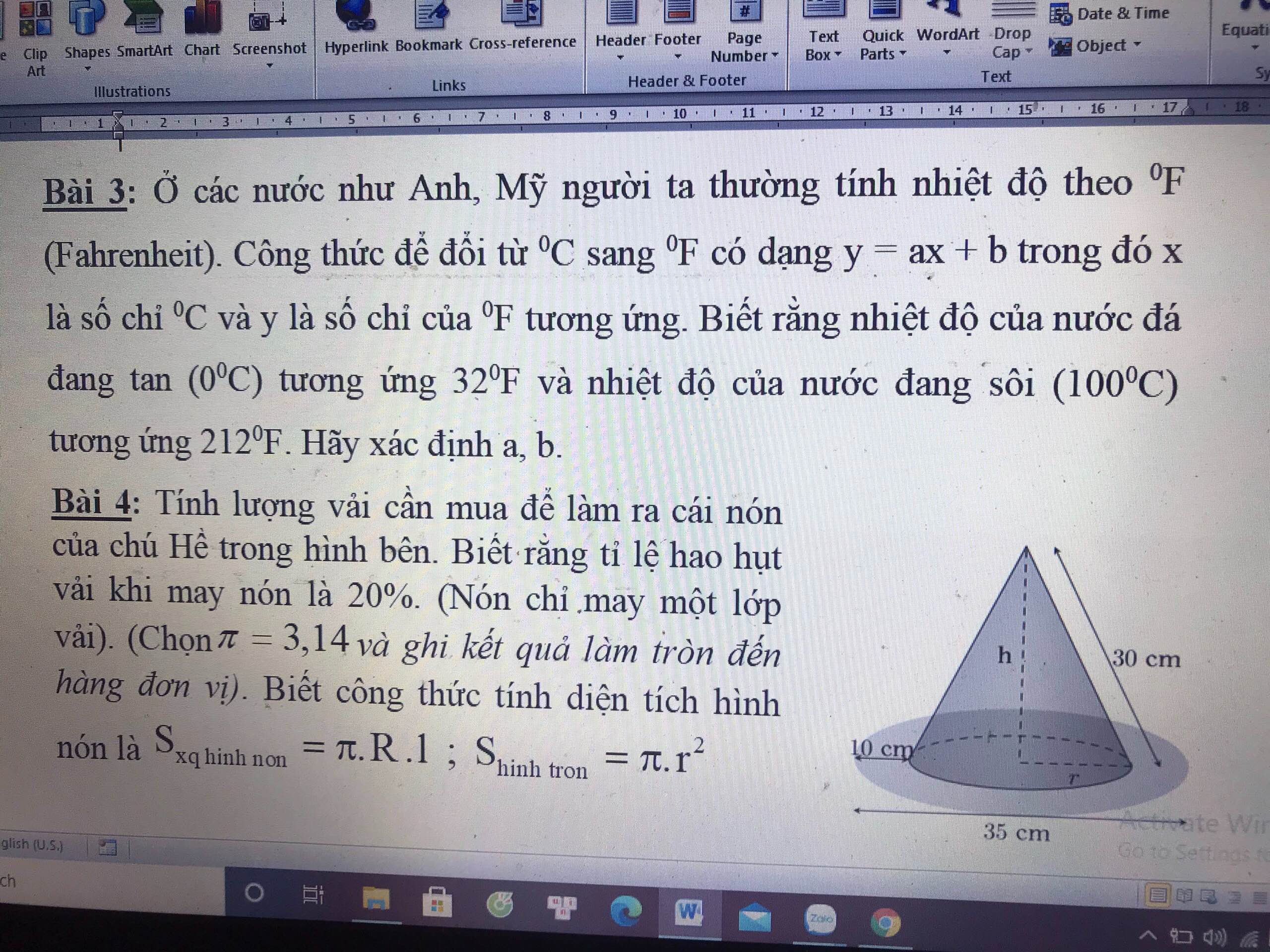
a)Ta có:
`hat{BFC}` là góc chẵn nửa (O)
`=>hat{BFC}=90^o`
Tương tự:`hat{BEC}=90^o`
Xét tam giác ABC có:
`CFbotAB(CMT)`
`AEbotAC(CMT)`
Mà CF cắt BE tại H
`=>H` là trực tâm tam giác ABC
`=>AHbotBC`
Hay `AD bot BC`
Vì `hat{BFH}=hat{BDH}=90^o`
`=>hat{BFH}+hat{BDH}=180^o`
`=>` tg BFHD nt
`=>hat{DFC}=hat{DBE}`
b)Vì `hat{EBC}=hat{EFC}`(cùng chắn cung EC nhỏ)
Mà tg BFHD nt
`=>hat{DFH}=\hat{HBD}`
`=>hat{DFH}=hat{EFC}`
`=>` FC là pg `hat{EFD}`
Vì `FC` là pg `hat{EFD}`
`=>hat{EFD}=2hat{DFH}`
Mà `hat{DFH}=hat{HBD}`
`=>hat{EFD}=2hat{DBH}`
Mà `hat{EOC}=2hat{DBH}`(góc nội tiếp và góc ở tâm)
`=>hat{EFD}=hat{EOC}`
`=>` tg OEFD nt (do trong = góc ngoài tại đỉnh đối)