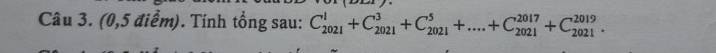a.
Qua S kẻ đường thẳng d song song AB
Do \(\left\{{}\begin{matrix}AB\in\left(SAB\right)\\CD\in\left(SCD\right)\\AB||CD\\S\in\left(SAB\right)\cap\left(SCD\right)\end{matrix}\right.\)
\(\Rightarrow d=\left(SAB\right)\cap\left(SCD\right)\)
b.
Gọi E là trung điểm AD, kéo dài AG cắt SD tại F \(\Rightarrow F\) là trung điểm SD (do G là trọng tâm SAD)
AM thuộc AB nên AM cắt SB tại B \(\Rightarrow B'\) trùng B
Trong mp (SCD), qua F kẻ đường thẳng song song CD cắt SC tại C'
\(\Rightarrow C'\) là trung điểm SC (do F là trung điểm SD)
Trong mp (ABCD), kéo dài AB và CE cắt nhau tại H
3 mp (SCE), (ABCD), (AGM) cắt nhau theo 3 giao tuyến phân biệt AB, CE, C'G, mà AB và CE cắt nhau tại H \(\Rightarrow\) 3 đường thẳng đồng quy tại H (theo t/c giao tuyến 3 mp cắt nhau)
Hay C',G,H thẳng hàng
\(AE||CB\) ; \(AE=\dfrac{1}{2}AD=\dfrac{1}{2}CB\Rightarrow\) AE là đường trung bình tam giác HCB
\(\Rightarrow A\) là trung điểm BH và E là trung điểm CH
\(\Rightarrow G\) là trọng tâm tam giác SCH
\(\Rightarrow\dfrac{HG}{HC'}=\dfrac{2}{3}\) (1)
Theo giả thiết \(MB=2MA\Rightarrow AB-MA=2MA\Rightarrow MA=\dfrac{1}{3}AB=\dfrac{1}{3}AH\)
\(\Rightarrow\dfrac{HM}{BH}=\dfrac{AH+AM}{2AH}=\dfrac{AH+\dfrac{1}{3}AH}{2AH}=\dfrac{2}{3}\) (2)
(1);(2) \(\Rightarrow\dfrac{HG}{HC'}=\dfrac{HM}{BH}\Rightarrow MG||BC'\)
Hay \(MG||B'C'\) (do B trùng B')









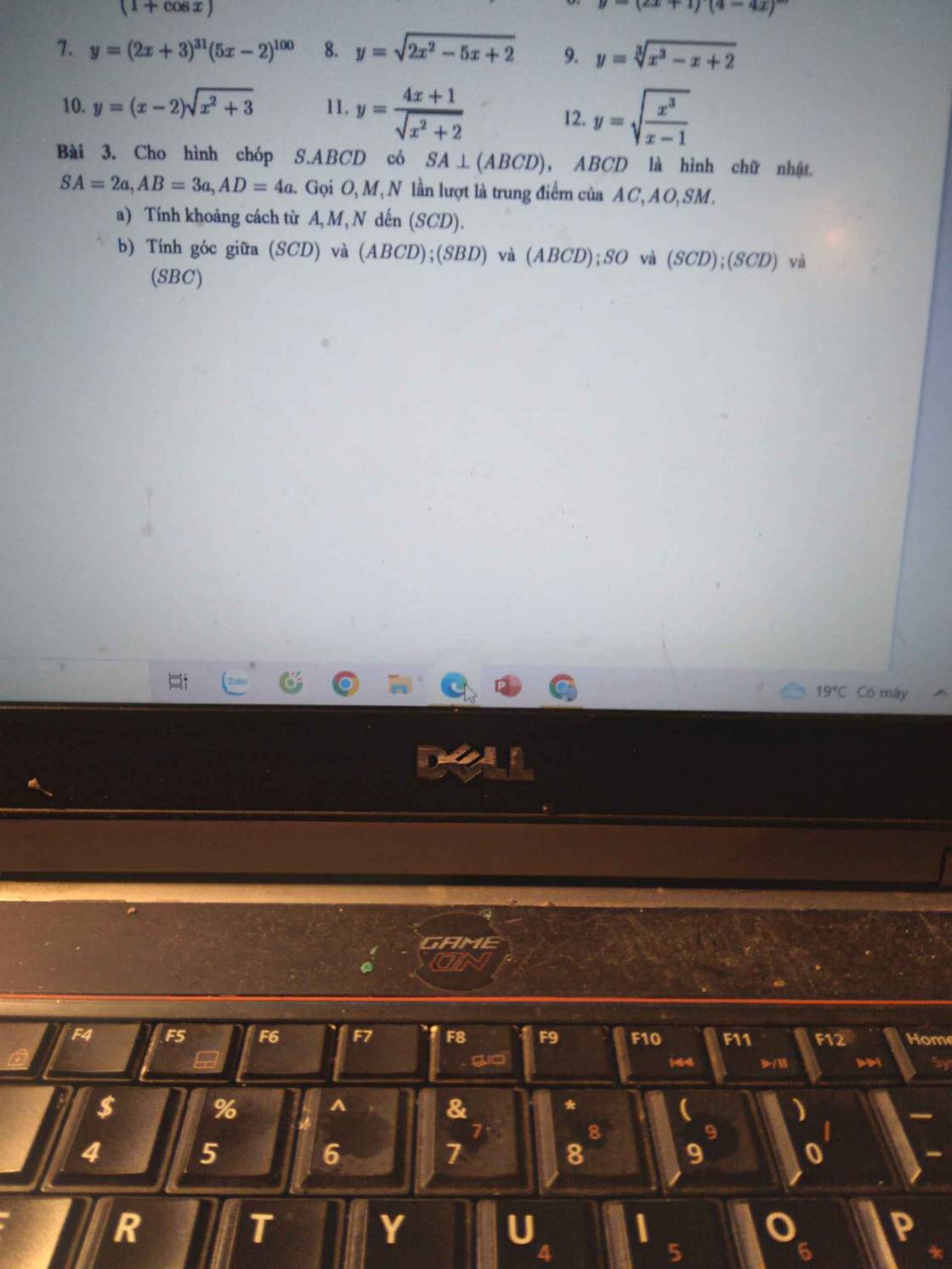 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ