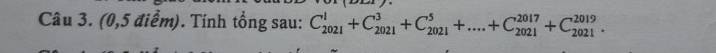a: AD vuông góc CD
SA vuông góc CD
=>CD vuông góc (SAD)
Kẻ AH vuông góc SD
=>CD vuông góc AH
mà SD vuông góc AH
nên AH vuông góc (CDS)
=>d(A;(SCD))=AH=căn (4a^2+16a^2/8a^2)=căn 10/2
Kẻ MP//AB//CD
=>AP/AD=AM/AC
=>AP/4a=1/4
=>AP=a
=>PD=3a
PQ vuông góc SD
PQ vuông góc CD
=>PQ vuông góc (SCD)
mà PM//(SCD)
nên d(P;(SCD))=PQ
Xét ΔADH có PQ/AH=PD/AD
\(\dfrac{PQ}{\sqrt{10}:2}=\dfrac{3a}{4a}=\dfrac{3}{4}\)
=>PQ=3 căn 10/8
=>d(M;(SCD))=PQ=3căn 10/8
Kẻ NG//AM
Kẻ GU vuông góc SD
=>d(G;(SCD))=GU
GU/AH=SG/SA=1/2
=>GU=căn 10/4
b: (SCD;ABCD))=(AD;SD)=góc ADH
AH=AD*cosADH
=>cosADH=căn 10/8
=>góc ADH=67 độ
(SBD;(ABCD))=góc SOA
SA=AO*tan SOA
=>tan SOA=2/5
=>góc SOA=22 độ

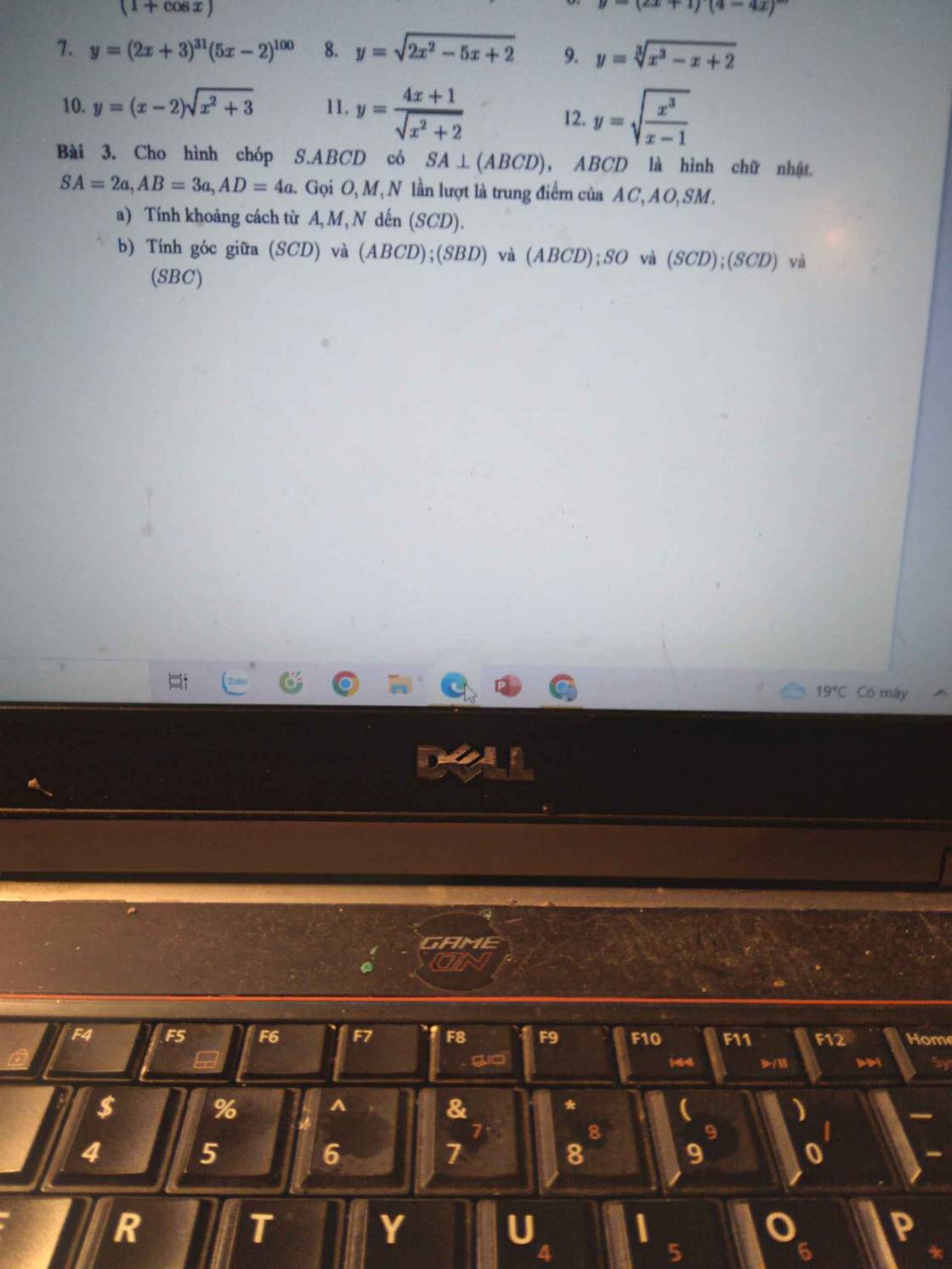 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ








 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ