Cho hàm số \(y=-\dfrac{1}{2}x^2\). Khảo sát đồ thị hàm số trên
Những câu hỏi liên quan
Cho hàm số: \(y=-\dfrac{1}{2}x^2\).Khảo sát và vẽ đồ thị (P) của hàm số trên
Tập xác định : R
Chiều biến thiên : hàm số đồng biến trên \(\left(-\infty;0\right)\)
hàm số nghịch biến trên \(\left(0;+\infty\right)\)
Lập bảng giá trị để vẽ đồ thị
Đúng 1
Bình luận (0)
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Cho hàm số \(y=\dfrac{1}{2}x^2\)
1) Khảo sát và vẽ đồ thị (P) của hàm số.
2) Cho A B, là hai điểm nằm trên đồ thị (P) lần lượt có hoành độ là -1 và +2.
a) Viết phương trình đường thẳng d đi qua A và có hệ số góc bằng \(\dfrac{1}{2}\)
b) Chứng tỏ điểm B cũng nằm trên đường thẳng d.
Cho hàm số \(y=\dfrac{1}{2}x^2\)
1) Khảo sát và vẽ đồ thị (P) của hàm số.
2) Cho A B, là hai điểm nằm trên đồ thị (P) lần lượt có hoành độ là -1 và +2.
a) Viết phương trình đường thẳng d đi qua A và có hệ số góc bằng \(\dfrac{1}{2}\)
b) Chứng tỏ điểm B cũng nằm trên đường thẳng d.
Câu 1: Cho hàm số y-125x^2a) Khảo sát tính đơn điệu của hàm số b) Tìm giá trị của m, n để các điểm A(1;m) và B (n; 125) thuộc đồ thị hàm số trênCâu 2: Cho hàm số y( m+1)x^2a) Xác định m để đồ thị hàm số đi qua điểm A (1;2)b) Vẽ đồ thị hàm số vừa tìm đượcc) Tìm điểm thuộc parapol nói trên có hoành độ bằng -2d) Tìm điểm thuộc parapol nói trên có tung độ bằng -8d) Tìm điểm thuộc parapol nói trên có tung độ gấp ba lần hoành độ
Đọc tiếp
Câu 1: Cho hàm số y=-125x\(^2\)
a) Khảo sát tính đơn điệu của hàm số
b) Tìm giá trị của m, n để các điểm A(1;m) và B (n; 125) thuộc đồ thị hàm số trên
Câu 2: Cho hàm số y=( m+1)x\(^2\)
a) Xác định m để đồ thị hàm số đi qua điểm A (1;2)
b) Vẽ đồ thị hàm số vừa tìm được
c) Tìm điểm thuộc parapol nói trên có hoành độ bằng -2
d) Tìm điểm thuộc parapol nói trên có tung độ bằng -8
d) Tìm điểm thuộc parapol nói trên có tung độ gấp ba lần hoành độ
Câu 2:
a) Để đồ thị hàm số \(y=\left(m+1\right)x^2\) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số \(y=\left(m+1\right)x^2\), ta được:
m+1=2
hay m=1
Vậy: m=1
Đúng 0
Bình luận (0)
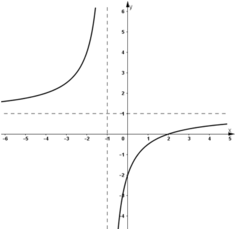
Cho hàm số y = x - 2 x + m - 1
Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số khi m = 2
Với m = 2 ta có hàm số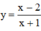 
- Tập xác định : D = R\{-1}.
- Sự biến thiên :
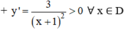
⇒ Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞).
+ Cực trị : hàm số không có cực trị
+ Tiệm cận :
⇒ y = 1 là tiệm cận ngang của đồ thị hàm số
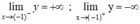
⇒ x = -1 là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên :
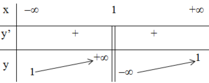
- Đồ thị :
Đúng 0
Bình luận (0)
a) khảo sát và vẽ đồ thị hàm số \(y=x^4-2x^2+3\)
b) vẽ đồ thị hàm số \(y=\left|x^4-2x^2+3\right|\)
Cho hàm số y = 2 x 4 − 4 x 2 (1). Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).
Tập xác định: D = R
y′=0 ⇔ 
Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; + ∞ )
Hàm số nghịch biến trên mỗi khoảng (− ∞ ; −1); (0; 1)
Hàm số đạt cực đại tại x = 0; y CĐ = 0
Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; y CT = −2
Đồ thị có hai điểm uốn:
Bảng biến thiên:
Đồ thị:
Đồ thị cắt trục hoành tại
Đúng 0
Bình luận (0)