Giúp mk bài III và bài I phần D ạ

Những câu hỏi liên quan
Giúp mk phần B bài III với ạ 😢
Bài điền T và F nhưng là phần B ạ
1. On the ocean
2. Yes
3. do house work , cleaning the floor , cooking meals , washing clothes , feeding his pets .
Đúng 0
Bình luận (0)
Mn ơi giúp mk bài III phần B dc ko ạ
1 Yes, there are
2 The city changed a lot
3 It's always sunny
Đúng 4
Bình luận (0)
Các bạn có thể làm ngay giúp mk bài III đến bài VI đc ko ạ
mk đang cần gấp ạ

Làm bài III, I và II giúp với ạ đang cần gấp . Thanks 


Ai giúp mình câu b phần 2 bài III với cả câu b bài IV với ạ. Mình xin cảm ơn rất rất nhiều ạ.

Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
Đúng 3
Bình luận (0)
Bài IV.b.
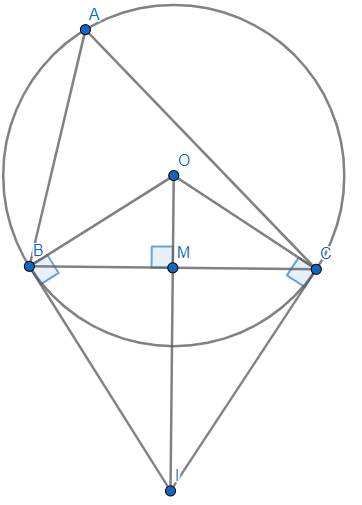
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
Đúng 2
Bình luận (0)
Giải giúp mk bài I,II ,III
Xem thêm câu trả lời
Giúp mk bài I và II ạ
1B
2A
3B
4B
5D
6A
7B
8B
9D
10B
1 are
2 taught
3 will be - makes
4 is sleeping
5 building (dream of Ving: mơ ước được làm gì)
Đúng 1
Bình luận (0)
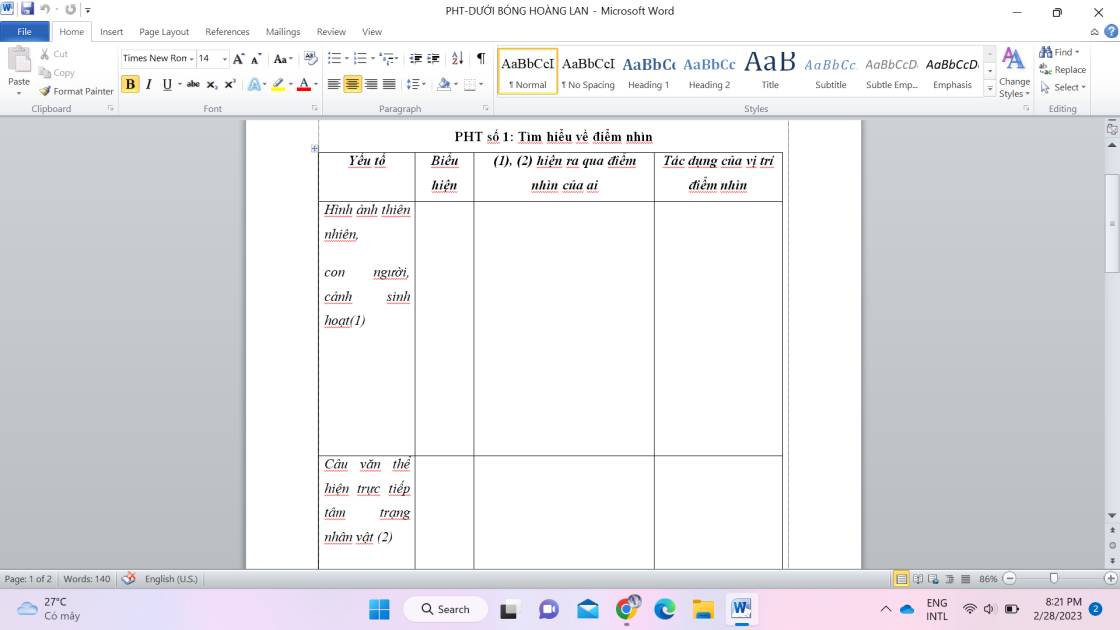
Câu hỏi này nằm trong bài Dưới bóng hoàng lan. Giúp mk trả lời phần này với ạ và cảm ơn ạ
Lời khuyên chân thành là em nên đọc kĩ bài, phần cô giáo phân tích trên lớp để làm, như vậy em vừa hiểu kĩ bài vừa là tự em sẽ rèn được kĩ năng làm bảng
Đúng 2
Bình luận (0)
 Các bạn giúp mk mỗi bài 3 phần b với phần c hoi ạ><
Các bạn giúp mk mỗi bài 3 phần b với phần c hoi ạ><
Mk cám mơn:))
Bài 3:
b: \(B_1=-\left|2x-3\right|+2\le2\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
\(B_2=-\left|x+4\right|+5\le5\forall x\)
Dấu '=' xảy ra khi x=-4
Đúng 2
Bình luận (0)
Bài 3:
b) Xét số \(-B_3=6+\left|x+4\right|\ge6\Rightarrow B_3\le-6\)
Dấu '=' xảy ra \(\Leftrightarrow x=-4\)
Đúng 2
Bình luận (0)
\(3,\\ b,B_1=2-\left|3-2x\right|\le2\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(B_2=5-\left|x+4\right|\le5\)
Dấu \("="\Leftrightarrow x=-4\)
\(B_3=-6-\left|x+4\right|\le-6\)
Dấu \("="\Leftrightarrow x=-4\)
\(c,15-\left(x^2-4\right)^2-\left|x+2\right|\le15\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x^2-4=0\\x+2=0\end{matrix}\right.\Leftrightarrow x=-2\)
\(C_2=10-\left|2x-1\right|-\left|y+x\right|\le10\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-\dfrac{1}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)


























