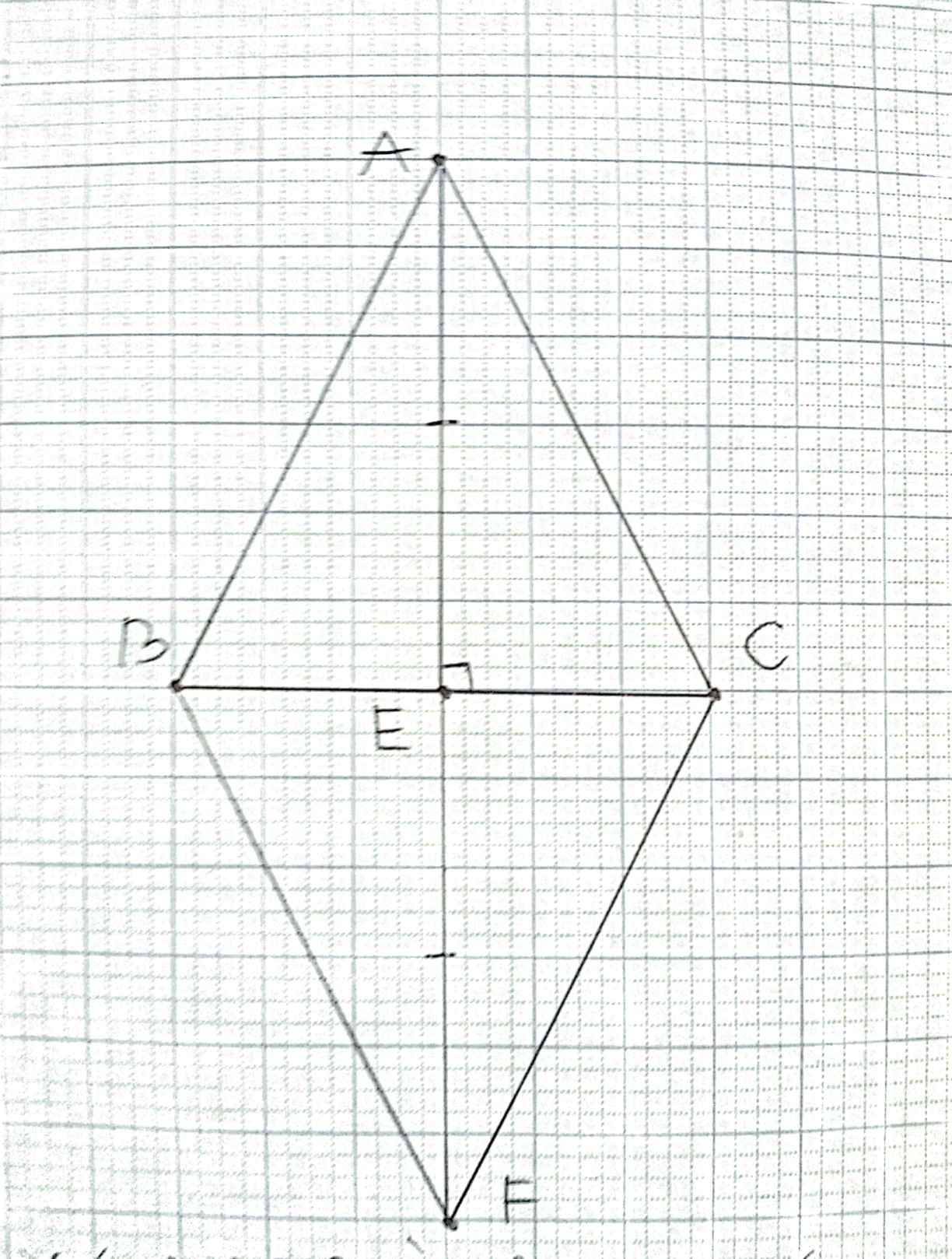
 Chứng minh AC//BF
Chứng minh AC//BF

Những câu hỏi liên quan
Cho ΔABC (AB=AC). Trên cạnh AB lấy E, trên cạnh AC lấy F sao cho AE=AF a) chứng minh BÉ= CF và CE=BF b) chứng minh BC//BF c) gọi Ở là giao của BF và CE. Chứng minh AO vuông góc với BC
a: Ta có: AE+EB=AB
AF+FC=AC
mà AE=AF
và AB=AC
nên BE=CF
Xét ΔABF và ΔACE có
AB=AC
góc BAF chung
AF=AE
Do đó: ΔABF=ΔACE
Suy ra: BF=CE
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
=>OB=OC
mà AB=AC
nên AO là đường trung trực của BC
Đúng 1
Bình luận (0)
Cho tam giác BFC có BF=BC. Lấy điểm E thuộc BC. Lấy điểm A thuộc BF sao cho BE =BA
a,Chứng minh EF=AC
b, Gọi EF cắt AC tại D. Chứng minh BD là tia phân giác góc FNC
C, Chứng minh AE//FC
N đâu ra thế bạn, câu b
Cho Δ ABC vuông ở A (AB < AC ). Vẽ tia phân giác góc B cắt cạch AC ở D. Trên BC lấy điểm E sao cho BE = BA
a) Chứng minh: Δ ABD = △ EBD
b) Chứng minh: DE ⊥ BC
c) Qua B vẽ BF ⊥ AB tại B và BF = AC
Chứng minh: BF // AC
Chứng minh: △ ABC = △ FCB
Các bạn giúp mình nhe nếu vẽ được hình càng tốt
a) Chứng minh: △ABD = △EBD
Xét △ABD và △EBD có
AB = BE ( giả thuyết )
Góc B1 = góc B2 ( BD là tia phân giác của góc ABC )
BD: cạch chung
⇒ △ABD = △EBD ( c-g-c )
b) Chứng minh: DE ⊥ BC
Vì △ABD = △EBD ( chứng minh trên )
⇒ Góc BAD = góc BED = 900 ( 2 góc tương ứng )
⇒ Góc BED = 900
Vậy DE ⊥ BC
c) Chứng minh: BF // AC
Ta có AC ⊥ AB ( △ ABC vuông tại A )
Mà BF ⊥ AB ( giả thuyết )
⇒ AC // BF
Chứng minh: △ABC = △FCB
Ta có AC // BF ( chứng minh trên )
⇒ Góc ACB = góc FBC ( so le trong )
Xét △ABC và △FCB có
AC = FB ( giả thuyết )
Góc ACB = góc FCB ( chứng minh trên )
BC: cạch chung
Vậy △ABC = △FCB
Chúc bạn học tốt ![]()
Cho tam giác ABC nhọn ( AB khác AC ). Trên nửa mặt phẳng bờ AB chứa C vẽ tia AE vuông góc với AB và AE AB, trên nửa mặt phẳng bờ AC chứa B Vẽ tia AF vuông góc với AC và AF AC
a) Chứng minh BF CE
b) Chứng minh BF vuông góc với DE
c) Vẽ AH vuông góc với BC( H thuộc BC) chứng minh AH đi qua trung điểm của EF
d) Vẽ AK vuông góc với EF( K thuộc EF) chứng minh AK đi qua trung điểm của BC
e) M là trung điểm của BC chứng minh AM vuông góc với EF
f) N là trung điểm của EF chứng minh AN vuông góc...
Đọc tiếp
Cho tam giác ABC nhọn ( AB khác AC ). Trên nửa mặt phẳng bờ AB chứa C vẽ tia AE vuông góc với AB và AE = AB, trên nửa mặt phẳng bờ AC chứa B Vẽ tia AF vuông góc với AC và AF = AC
a) Chứng minh BF = CE
b) Chứng minh BF vuông góc với DE
c) Vẽ AH vuông góc với BC( H thuộc BC) chứng minh AH đi qua trung điểm của EF
d) Vẽ AK vuông góc với EF( K thuộc EF) chứng minh AK đi qua trung điểm của BC
e) M là trung điểm của BC chứng minh AM vuông góc với EF
f) N là trung điểm của EF chứng minh AN vuông góc với BC
Xem thêm câu trả lời
cho tam giác ABC, D là trung điểm của AC .Trên tia đối của tia BA lấy E sao cho BE = BA. Trên nửa mặt phẳng chứa C có bờ là AB vẽ BF // AC và BF = AC/2
a) Chứng minh EF = BD
b) Chứng minh F là TĐ của EC
ChoDeltaABC có ABAC.Gọi E;F lần lượt là các điểm trên AB,AC sao cho AEAFa)Chứng minh BFCE (0,5đ)b)Gọi I là giao điểm của BF và CE Chứng minhDeltaBIEDeltaCIF (0,5đ)c)Chứng minh AI là phân giác củastackrelfrown{BAC} (0,5đ)d)Kéo dài AI cắt BC tại H Chứng minh AHperpBC (0,5đ)e)Chứng minh EF//BC (0,5đ)Vẽ hình ghi giả thiết kết luận (0,5đ)
Đọc tiếp
Cho\(\Delta\)ABC có AB=AC.Gọi E;F lần lượt là các điểm trên AB,AC sao cho AE=AF
a)Chứng minh BF=CE (0,5đ)
b)Gọi I là giao điểm của BF và CE
Chứng minh\(\Delta\)BIE=\(\Delta\)CIF (0,5đ)
c)Chứng minh AI là phân giác của\(\stackrel\frown{BAC}\) (0,5đ)
d)Kéo dài AI cắt BC tại H
Chứng minh AH\(\perp\)BC (0,5đ)
e)Chứng minh EF//BC (0,5đ)
Vẽ hình ghi giả thiết kết luận (0,5đ)
a: Xét ΔABF và ΔACE có
AB=AC
\(\widehat{A}\) chung
AF=AE
Do đó: ΔABF=ΔACE
Đúng 0
Bình luận (0)
cho tam giác abc nhọn
vẽ phía ngoài tam giác abc:
AE vuông góc với AB; AE=AB
AF vuông góc với AC; AF=AC
a,Chứng minh BF=CF
b,Chứng minh BF vuông góc với CF
Cho hình bình hành ABCD. Trên đường chéo AC lấy E và F sao cho AE = EF = FC
a) Chứng minh: BFDE - hình bình hành
b) Vẽ tia BF cắt CD tại M. Chứng minh: BF = 2FM
Bạn tự vẽ hình nha
Xét \(\Delta ADE\)và \(\Delta CBF\):
\(AD=BC\left(ABCD-hbh\right)\)
\(AF=FC\left(gt\right)\)
\(\widehat{DAC}=\widehat{ACB}\)( slt , AD // BC )
\(\Rightarrow\)\(\Delta ADE=\Delta CBF\left(c-g-c\right)\)
\(\Rightarrow\)\(DE=FB\)( 1 )
Xét \(\Delta AEB\)và \(\Delta CFD\):
\(AB=CD\left(ABCD-hbh\right)\)
\(AE=FC\left(gt\right)\)
\(\widehat{CAB}=\widehat{DCA}\)( slt , AB // CD )
\(\Rightarrow\)\(\Delta AEB=\Delta CFD\left(c-g-c\right)\)
\(\Rightarrow\)\(EB=FD\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra BFDE - hbh ( đpcm )
b) \(\Delta ECD\)có :
\(EF=FC\left(gt\right)\)
MF // DE ( Vì BF // DE , M thuộc BF )
\(\Rightarrow\)FM - đtb của tam giác ECD
\(\Rightarrow\)ED = 2FM
Mà ED = BF ( Vì BFDE - hbh )
\(\Rightarrow\)BF = 2FM ( đpcm )
Đúng 0
Bình luận (0)
tích mình với
ai tích mình
mình tích lại
thanks
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB>AC và AD là tia pg trên AB lấy F sao cho AC=AF lấy điểm E tuy ý chứng minh
1, tam giác AEC=AEF
2, AB-AC=BF
3, BE-EC<BF
Điểm E tùy ý nhưng nằm ở khu vực nào vậy bạn?
Đúng 0
Bình luận (0)





















