Ai giải thích giúp mình tại sao trên là P =x/x-3 mà dưới lại là P=x-3+3/x-3 với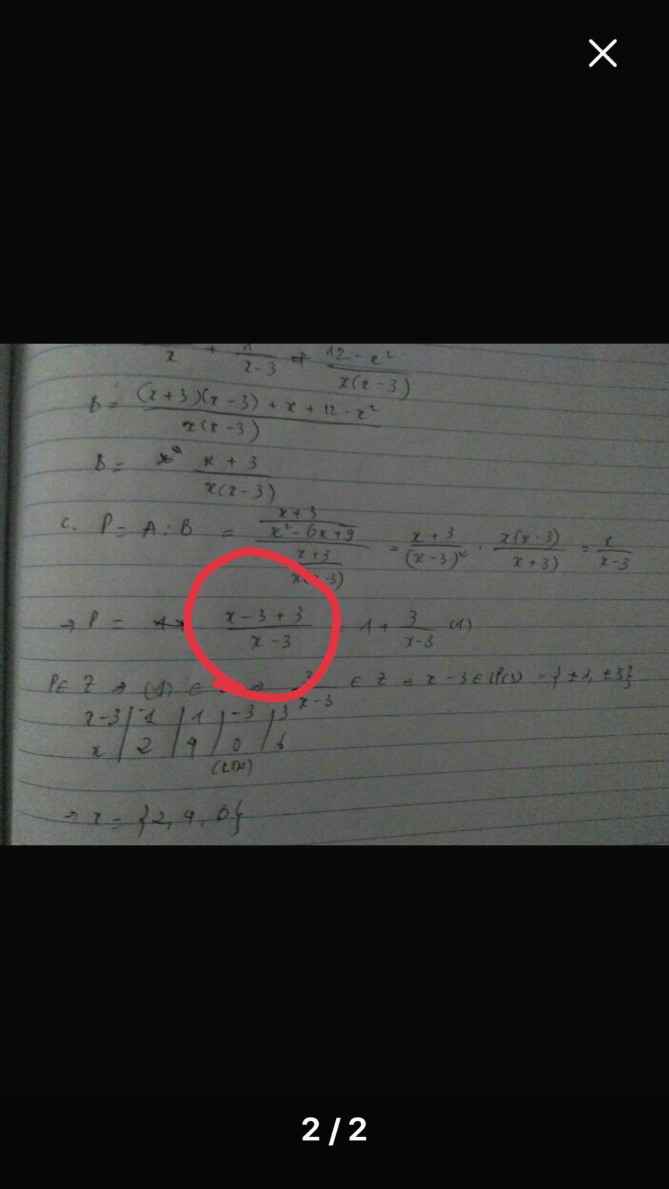

Những câu hỏi liên quan
Giúp mình giải thích:
<=> 2(x^2 + 2.3.x + 9) +2
<=> 2 (x+3)^2 + 2
Tại sao lại ...? ak mà thôi, phân tích cực kì chi tiết là mk hỉu
Làm nhanh nhất mình tik nhé!
\(x^2+2.3.x+9\) là hẳng đẳng thức số 1 sau khi phân tích
\(\left(x+3\right)^2=x^2+2.3.x+9\)
Hiểu chưa , Chúc em học tốt
Mà cái này lớp mà
Đúng 0
Bình luận (0)
ko hiểu anh ạ, em chỉ cần anh phân tích (Làm thêm 1 số bước tách ra) làm sao cho cái trên (2(x^2 + 2.3.x + 9) +2) bằng cái dưới
Đúng 0
Bình luận (0)
Ta có: \(2\left(x^2+2.3x+9\right)+2=2\left(x^2+2.3x+3^2\right)+2=2\left(x+3\right)^2+2\)(Áp dụng hằng đẳng thức)
Ngược lại ta cũng có: \(2\left(x+3\right)^2+2=2\left(x+3\right)\left(x+3\right)+2\)
Mặt khác: \(\left(x+3\right)\left(x+3\right)=x\left(x+3\right)+3\left(x+3\right)=x.x+x.3+3.x+3.3=x^2+3x+3x+9\)
\(=x^2+2.3x+9\)
Khi đó: \(2\left(x+3\right)\left(x+3\right)+2=2\left(x^2+2.3x+9\right)+2\)
Vậy \(2\left(x^2+2.3x+9\right)+2=2\left(x+3\right)^2+2\)
(Vì cần áp dụng hằng đẳng thức nên mình nghĩ đây là bài tập lớp 8 nha bạn)
Đúng 0
Bình luận (0)
giá trị tuyệt đối là x dương thì |x| = x, còn x âm thì |x| = -x. Vậy, tại sao khi |\(\sqrt{5}\)-3| = 3 - \(\sqrt{5}\)???
vì 3 là -3 thì -(-3) là thành + 3 còn \(\sqrt{5}\) là dương mà sao thành âm? giúp với!!!
ai đúng mình sẽ like
\(\sqrt{5}< \sqrt{9}=3\Leftrightarrow\sqrt{5}-3< 0\\ \Leftrightarrow\left|\sqrt{5}-3\right|=-\left(\sqrt{5}-3\right)=3-\sqrt{5}\left(đpcm\right)\)
Đúng 1
Bình luận (1)
Lý do rất đơn giản: |a| = -a khi a < 0. Vì \(\sqrt{5}\) < 3 nên giá trị của \(\sqrt{5} - 3\) < 0. Khi lấy giá trị tuyệt đối của \(\sqrt{5} - 3\) thì sẽ được kết quả là \(-(\sqrt{5} - 3)\) (vì \(\sqrt{5} - 3\) < 0 như đã nêu trên). Mà \((a - b) = -(b - a)\) và ngược lại, nên \(-(\sqrt{5} - 3)\) = \(3 - \sqrt{5}\). Vậy \(|\sqrt{5} - 3| = 3 - \sqrt{5}\).
Mình biết lý do tại sao bạn bị rối ở chỗ này. Đó là vì bạn nghĩ rằng khi lấy giá trị tuyệt đối của một biểu thức thì kết quả sẽ là biểu thức mới bao gồm giá trị tuyệt đối của từng số hạng, thế nên mình đã chứng minh cho bạn thấy là bạn đang bị sai.
Đúng 1
Bình luận (1)
Rút gọn biểu thức : b) xn-1 ( x + y ) - y ( xn-1 + yn-1 )
Các bạn giải thích giúp mình với mà kiểu như tại sao lại ra như vậy ấy tại mình muốn hiểu chứ hk phải câu trả lời _ Thanks <3 <3 <3
xn-1(x+y)-y(xn-1+yn-1)
=xn-1+1+xn-1y-xn-1y-yn-1+1
=xn+xn-1y-xn-1y-yn
=xn-yn
Đúng 0
Bình luận (0)
1.phép biến đổi tương đương nào là đúng?
A.Ix-3I = 3-x⇔3-x=0 B.Ix-3I = 3-x⇔3-x>0
C.Ix-3I = 3-x⇔3-x≤0 D..Ix-3I = 3-x⇔3-x≥0
CHỌN ĐÁP ÁN,GIẢI THÍCH TẠI SAO CHỌN ĐÁP ÁN ĐÓ GIÚP MÌNH VỚI Ạ BÀI NÀY MÌNH KH HIỂU
Giải phương trình: 3x-8/5 - 5 = 3-2(x+4)/2 lưu ý: 3-2(x+4) là tử nha
Ai giải hộ mình với mình làm đi làm lại mà vẫn không ra. Cám ơn nhaaa
Các Bạn không cần làm mà chỉ mình chỗ này mình chưa hiểu : Phần B Khi mà giải ra B = 4/( 3 - căn x) thì làm sao để biết được (3 - căn x) này là âm ạ. Hay cả trên tử cũng vậy (1+căn x) ( liên quan tới hình ảnh bên dưới) 
cái này thì ko nhất thiết phải Cm nha bạn
Câu b kêu tìm x để B ko nhỏ hơn hoặc bằng A
Nghĩa là
\(\dfrac{4}{3-\sqrt{x}}>1\)
\(\Leftrightarrow\dfrac{4}{3-\sqrt{x}}-1>0\)
\(\Leftrightarrow\dfrac{4-\left(3-\sqrt{x}\right)}{3-\sqrt{x}}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{3-\sqrt{x}}>0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}+1>0\\3-\sqrt{x}>0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}+1< 0\left(VL\right)\\3-\sqrt{x}< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Theo Đk ta có x≥0
Vậy 0≤x<9 thì B ko nhỏ hơn hoặc bằng A
Đúng 1
Bình luận (1)
Lời giải giống như bạn dưới đã viết.
Để $B$ không nhỏ hơn hoặc bằng $A$
Tức là $B>A$
$\Leftrightarrow \frac{4}{3-\sqrt{x}}>1$
$\Leftrightarrow \frac{4}{3-\sqrt{x}}-1>0\Leftrightarrow \frac{\sqrt{x}+1}{3-\sqrt{x}}>0$
Để phân thức này dương thì tử và mẫu phải cùng dấu.
Mà $\sqrt{x}+1\geq 0+1>0$ (dương rồi) nên $\sqrt{3}-x$ cũng dương.
------------------------
Đây là cách dễ làm nhất đối với bài này.
------------------------
Về phần lời giải của cô em, chị nghĩ trong lúc giảng em bị miss mất 1 số ý chứ ý cô không phải khẳng định mẫu âm đâu. Có lẽ ý của cô em thế này:
Khi em có: $\frac{4}{3-\sqrt{x}}>1$ thì em không nên nhân chéo mà nên trừ để đưa về hiệu >0 (như bạn Khoa đã giải). Nếu nhân chéo, em sẽ mắc phải 2 TH mẫu âm, mẫu dương như sau:
TH1: $3-\sqrt{x}>0$ thì $\frac{4}{3-\sqrt{x}}>1$ tương đương với $4> 3-\sqrt{x}$
TH2: $3-\sqrt{x}< 0$ thì tương đương $4< 3-\sqrt{x}$ (khi nhân 2 vế với số âm thì phải đổi dấu)
Như vậy thì rất là phức tạp. Nên để tránh TH mẫu âm mà hs giữ nguyên dấu khi nhân chéo thì cô em khuyên như vậy.
Đúng 0
Bình luận (0)
Em còn chỗ nào chưa hiểu thì cứ hỏi thoải mái.
Đúng 0
Bình luận (0)
Giái pt này giúp mình với
\(x^5+x^3-\sqrt{1-3x}+4=0\)
( mà có ai biết giải bằng phương pháp hàm số là sao ko ? )
Giải bằng phương pháp hàm số tức là sử dụng đạo hàm để khảo sát đặc điểm của hàm số (tính đơn điệu, cực trị, ... ) bạn nhé.
Đặt f(x)=\(x^5+x^3-\sqrt{1-3x}+4\) với tập xác định \(D=(-\infty;\frac{1}{3}]\)
Xét đạo hàm f'(x) = \(5x^4+3x^2+\frac{3}{2\sqrt{1-3x}}>0\)\(\forall x\in D\)
Từ đó suy ra hàm số y=f(x) đồng biến trên tập xác định D của nó. Suy ra hàm số NẾU có nghiệm thì chỉ có duy nhất một nghiệm.
Mà ta lại nhẩm được f(-1)=0. Vậy phương trình có nghiệm duy nhất \(x=-1\)
ai giải thích giúp mình câu này với ạgiả sử x, i là hai biến kiểu integer. Xét đoạn chương trình saux:2; For i:1 to 6 do if i mod 30 then x:x*i else x:x+i; Writeln (x);Đoạn chương trình trên sẽ in ra màn hình giá trị của x là
Đọc tiếp
ai giải thích giúp mình câu này với ạ
giả sử x, i là hai biến kiểu integer. Xét đoạn chương trình sau
x:=2; For i:=1 to 6 do if i mod 3=0 then x:=x*i else x:=x+i; Writeln (x);
Đoạn chương trình trên sẽ in ra màn hình giá trị của x là
Tìm số tự nhiên nhỏ nhất sao cho khi chia số đó cho 3 dư 1; chia cho 4 dư 2; chia cho 5 dư 3; chia cho 6 dư 4 và chia hết cho 11.giải thích từng chỗ nha Gọi số phải tìm là x.GiảiTheo bài ra ta có x + 2 chia hết cho 3, 4, 5, 6. x + 2 là bội chung của 3, 4, 5, 6Mà BCNN(3; 4; 5; 6) 60 nên x + 2 60.n .Do đó x 60.n – 2 ; (n 1; 2; 3.....)Mặt khác x11 nên lần lượt cho n 1; 2; 3.... Ta thấy n 7 thì x 418 11Vậy số nhỏ nhất phải tìm là 418.Mình k hỉu sao lại là x + 2 các bạn giải thích giùm mình n...
Đọc tiếp
Tìm số tự nhiên nhỏ nhất sao cho khi chia số đó cho 3 dư 1; chia cho 4 dư 2; chia cho 5 dư 3; chia cho 6 dư 4 và chia hết cho 11.
giải thích từng chỗ nha
Gọi số phải tìm là x.
Giải
Theo bài ra ta có x + 2 chia hết cho 3, 4, 5, 6.
=> x + 2 là bội chung của 3, 4, 5, 6
Mà BCNN(3; 4; 5; 6) = 60 nên x + 2 = 60.n .
Do đó x = 60.n – 2 ; (n = 1; 2; 3.....)
Mặt khác x11 nên lần lượt cho n = 1; 2; 3.... Ta thấy n = 7 thì x = 418 11
Vậy số nhỏ nhất phải tìm là 418.
Mình k hỉu sao lại là x + 2 các bạn giải thích giùm mình nha























