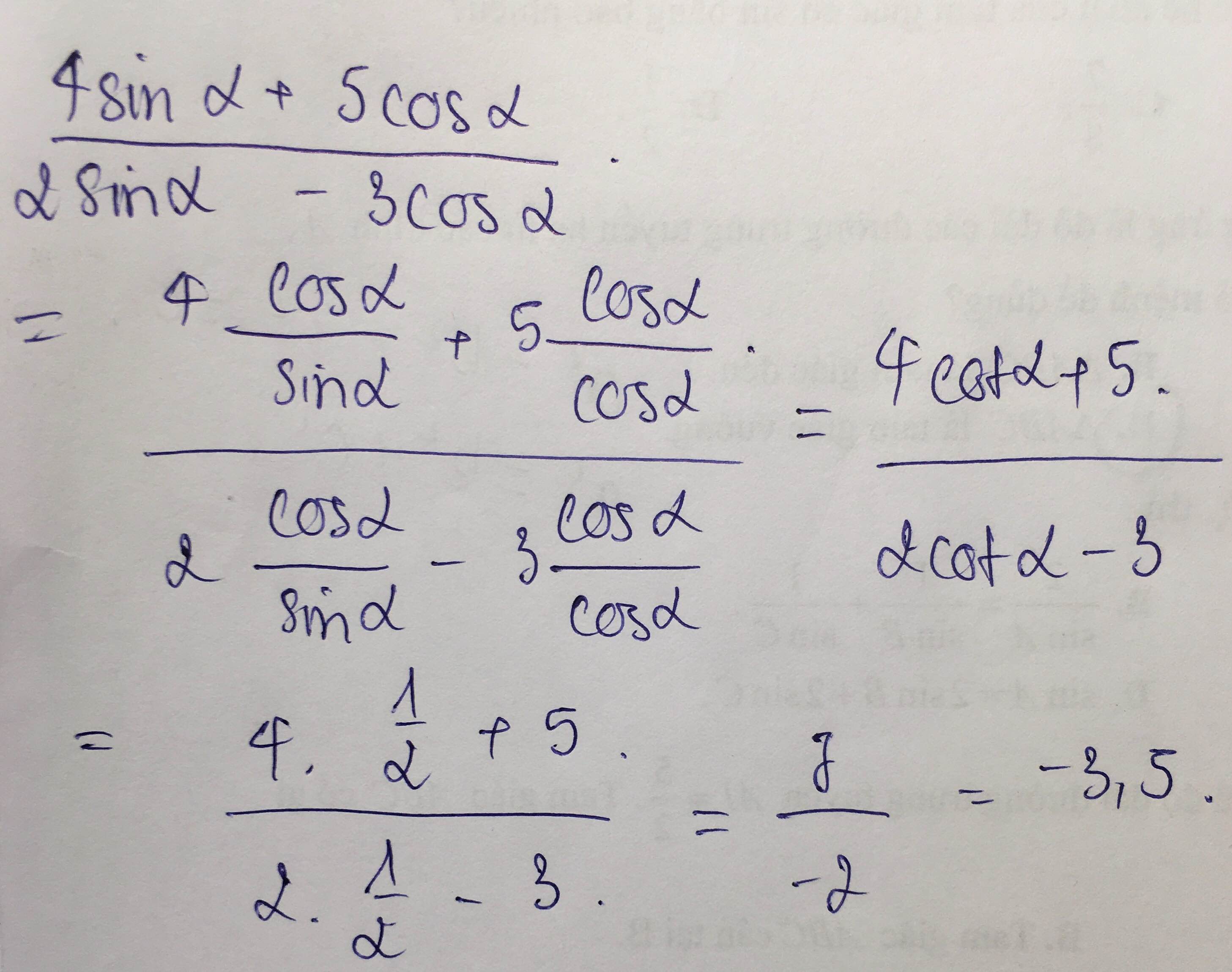Nếu sin alpha = 12 /13 thì tan alpha bằng bao nhiêu

Những câu hỏi liên quan
1/Rút gọn :
\(G=\left(1-sin^2x\right)cot^2x+1-cot^2x\)
2/ Nếu \(tan\alpha+cot\alpha=2\) thì \(tan^2\alpha+cot^2\alpha\) bằng bao nhiêu?
\(G=cot^2x-sin^2x.cot^2x+1-cot^2x=1-sin^2x.cot^2x\)
\(=1-sin^2x.\dfrac{cos^2x}{sin^2x}=1-cos^2x=sin^2x\)
2.
\(tana+cota=2\Rightarrow\left(tana+cota\right)^2=4\)
\(\Rightarrow tan^2a+cot^2a+2tana.cota=4\)
\(\Rightarrow tan^2a+cot^2a+2=4\)
\(\Rightarrow tan^2a+cot^2a=2\)
Đúng 1
Bình luận (0)
cho \(\cos\alpha=\dfrac{-12}{13}\) biết \(\pi< \alpha< \dfrac{3\pi}{2}\)
tính \(\sin\alpha,cos2\alpha,tan\left(\alpha-\dfrac{\pi}{3}\right),sin\left(2\alpha+\dfrac{\pi}{6}\right)\)
Có \(a\) thuộc góc phần tư thứ III -> sin\(a\) < 0
+) sin\(a\)=-\(\sqrt{1-cos^2a}\)=-\(\sqrt{1-\left(\dfrac{-12}{13}\right)^2}\)=\(\dfrac{-5}{13}\)
\(cos2a=cos^2a-sin^2a\)=\(\left(\dfrac{-12}{13}\right)^2-\left(\dfrac{-5}{13}\right)^2=\dfrac{119}{169}\)
Đúng 0
Bình luận (0)
Cho \(\sin \alpha = \frac{{12}}{{13}}\) và \(\cos \alpha = - \frac{5}{{13}}\). Tính \(\sin \left( { - \frac{{15\pi }}{2} - \alpha } \right) - \cos \left( {13\pi + \alpha } \right)\)
Ta có:
\(\begin{array}{l}\sin \left( { - \frac{{15\pi }}{2} - \alpha } \right) - \cos \left( {13\pi + \alpha } \right) = \sin \left( { -\frac{{16\pi }}{2} +\frac{{\pi }}{2} + \alpha } \right) - \cos \left( {12\pi + \pi + \alpha } \right) = \sin \left( {-8\pi + \frac{\pi }{2} - \alpha } \right) - \cos \left( { \pi + \alpha } \right) \\ = \sin \left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( \alpha \right) = \cos \left( \alpha \right) + \cos \left( \alpha \right) = 2\cos \left( \alpha \right) = 2.\left( { - \frac{5}{{13}}} \right) = \frac{{ - 10}}{{13}}\end{array}\)
Đúng 0
Bình luận (0)
Cho biết \(\tan\alpha=-3\). Giá trị của P = \(\frac{6\sin\alpha-7\cos\alpha}{6\cos\alpha+7\sin\alpha}\) bằng bao nhiêu?
Cho \(\tan\alpha=3.\)Chứng minh:
\(\frac{\sin^3\alpha-\cos^3\alpha}{\sin^3\alpha+\cos^3\alpha}=\frac{13}{14}\)
\(\frac{\sin^3\alpha-\cos^3\alpha}{\sin^3\alpha+\cos^3\alpha}=\frac{\frac{\sin^3\alpha}{\cos^3\alpha}-1}{\frac{\sin^3\alpha}{\cos^3\alpha}+1}=\frac{\tan^3\alpha-1}{\tan^3\alpha+1}=\frac{27-1}{27+1}=\frac{13}{14}\)
Đúng 0
Bình luận (0)
cho sin α =\(\frac{-5}{13}\) và \(\frac{3\pi}{2}\) < α < π . Tìm sin α , tan α , cot α
Ý bạn là \(\pi< a< \frac{3\pi}{2}\) và tìm \(cosa,tana,cota\)?
Khi đó \(cosa< 0\) \(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\frac{12}{13}\)
\(tana=\frac{sina}{cosa}=\frac{5}{12}\)
\(cota=\frac{1}{tana}=\frac{12}{5}\)
Đúng 0
Bình luận (0)
Biết cotα=1/2. Gía trị biểu thức A=\(\dfrac{4\sin\alpha+5\cos\alpha}{2\sin\alpha-3\cos\alpha}\) bằng bao nhiêu?
\(cot\alpha=\dfrac{1}{2}tacó:\)
\(cot\alpha=\dfrac{cos\alpha}{sin\alpha}\)
\(A=\dfrac{4sin\alpha+5cos\alpha}{2sin\alpha-3cos\alpha}\)
\(A=\dfrac{\dfrac{4sin\alpha}{sin\alpha}+\dfrac{5cos\alpha}{sin\alpha}}{\dfrac{2sin\alpha}{sin\alpha}-\dfrac{3cos\alpha}{sin\alpha}}\)
\(A=\dfrac{4+5cot\alpha}{2-3cot\alpha}\)
\(A=\dfrac{4+5\left(\dfrac{1}{2}\right)}{2-3\left(\dfrac{1}{2}\right)}\)
\(A=13\)
Đúng 1
Bình luận (0)
Biết cotα=1/2. Gía trị biểu thức A=\(\dfrac{4\sin\alpha+5\cos\alpha}{2\sin\alpha-3\cos\alpha}\) bằng bao nhiêu?
Cho tan\(\alpha\)=3. CMR :\(\frac{\sin^3\alpha-\cos^3\alpha}{\sin^3\alpha+\cos^3\alpha}\)= \(\frac{13}{14}\)