 cíu :((
cíu :((

Những câu hỏi liên quan

cíu cíu cíu
1 was repaired
2 Was - bought
3 are watered
4 wasn't learned
5 was watched
6 Is - read
7 was stolen
8 was broken
9 wasn't cut
10 is cleaned
Đúng 1
Bình luận (0)
Cíu cíu !!
\(n_{AgNO_3}=1.0,5=0,5\left(mol\right);n_{HCl}=2.0,3=0,6\left(mol\right)\)
PTHH: AgNO3 + HCl → AgCl ↓ + HNO3
Mol: 0,5 0,5 0,5
Ta có: \(\dfrac{0,5}{1}< \dfrac{0,6}{1}\)⇒ AgNO3 pứ hết, HCl dư
* Vdd sau pứ = 0,5+0,6 = 1,1 (l)
\(\Rightarrow C_{M_{ddNO_3}}=\dfrac{0,5}{1,1}=0,4545M\)
\(C_{M_{ddHCldư}}=\dfrac{0,6-0,5}{1,1}=0,0909M\)
\(m_{ddAgNO_3}=500.1,2=600\left(g\right);m_{ddHCl}=300.1,5=450\left(g\right)\)
* mdd sau pứ = 600+450 = 1050 (g)
\(C\%_{ddHNO_3}=\dfrac{0,5.63.100\%}{1050}=3\%\)
\(C\%_{ddHCl}=\dfrac{\left(0,6-0,5\right).36,5.100\%}{1050}=0,348\%\)
Đúng 0
Bình luận (3)
nAgNO3=1.0,5=0,5(mol);nHCl=2.0,3=0,6(mol)
PTHH: AgNO3 + HCl → AgCl ↓ + HNO3
Mol: 0,5 0,5 0,5
Ta có: \(\frac{0 , 5}{1} < \frac{0 , 6}{1}\)⇒ AgNO3 pứ hết, HCl dư
* Vdd sau pứ = 0,5+0,6 = 1,1 (l)
\(\Rightarrow C_{M_{d d N O_{3}}} = \frac{0 , 5}{1 , 1} = 0 , 4545 M\)
\(C_{M_{d d H C l d ư}} = \frac{0 , 6 - 0 , 5}{1 , 1} = 0 , 0909 M\)
\(m_{d d A g N O_{3}} = 500.1 , 2 = 600 \left(\right. g \left.\right) ; m_{d d H C l} = 300.1 , 5 = 450 \left(\right. g \left.\right)\)
* mdd sau pứ = 600+450 = 1050 (g)
\(C \%_{d d H N O_{3}} = \frac{0 , 5.63.100 \%}{1050} = 3 \%\)
\(C \%_{d d H C l} = \frac{\left(\right. 0 , 6 - 0 , 5 \left.\right) . 36 , 5.100 \%}{1050} = 0 , 348 \%\)
Đúng 0
Bình luận (0)
cíu cíu

Xem thêm câu trả lời
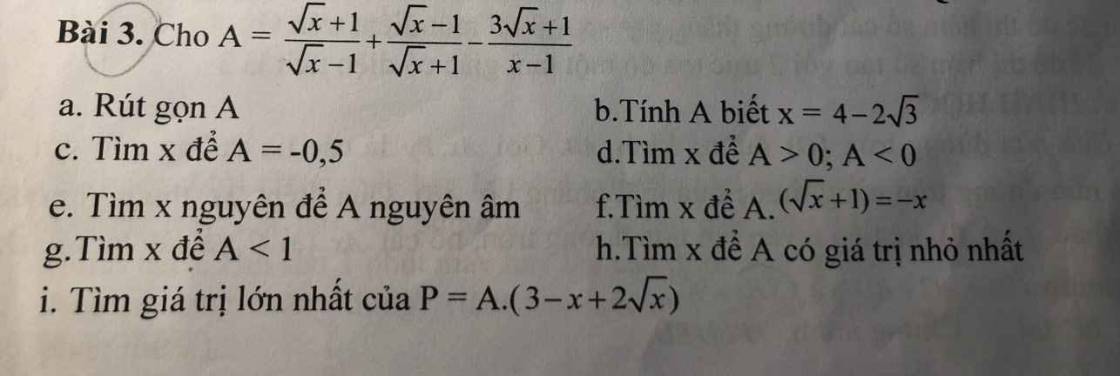 cíu cíu
cíu cíu
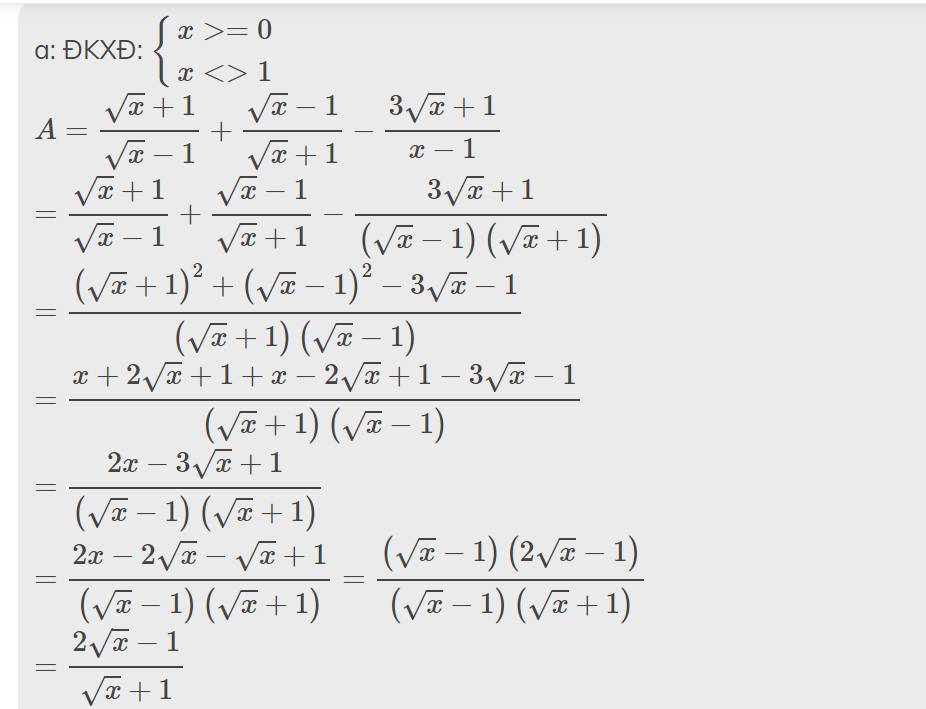
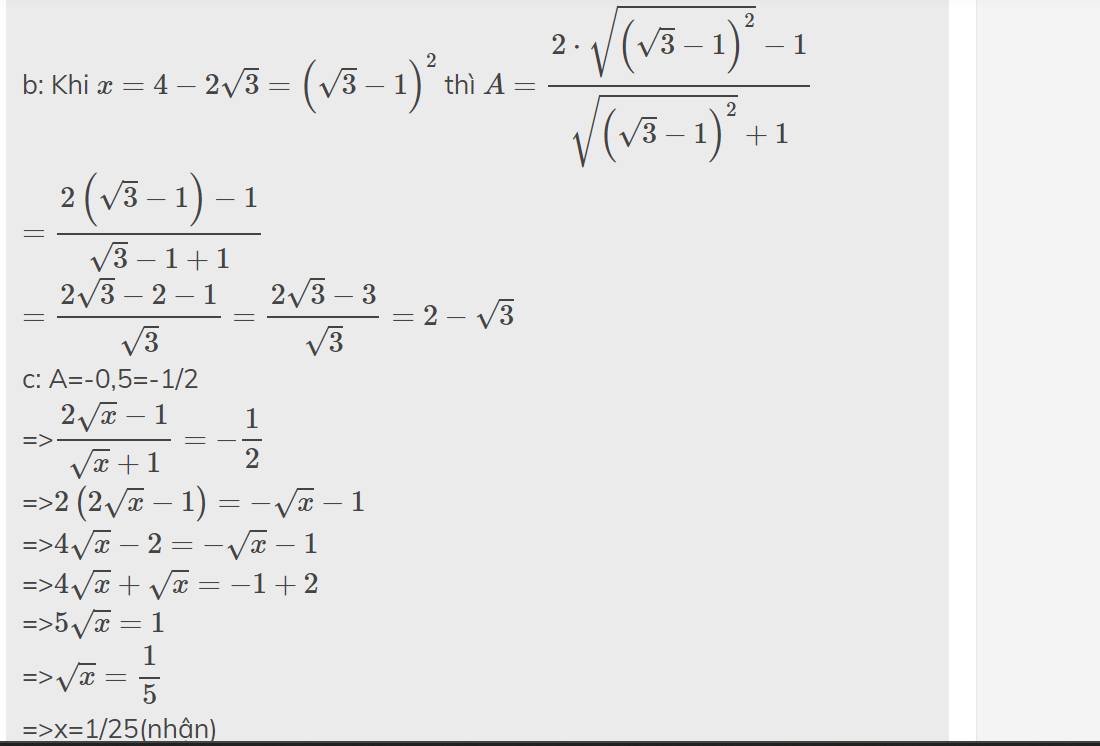

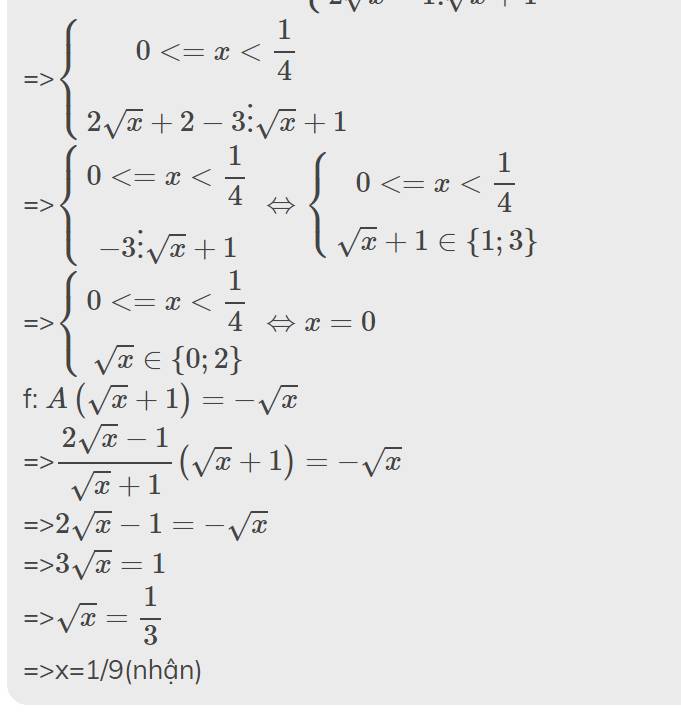
g: A<1
=>\(\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}< 1\)
=>\(\dfrac{2\sqrt{x}-1-\sqrt{x}-1}{\sqrt{x}+1}< 0\)
=>\(\sqrt{x}-2< 0\)
=>\(\sqrt{x}< 2\)
=>0<=x<4
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< =x< 4\\x< >1\end{matrix}\right.\)
h: \(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
=>\(A=\dfrac{2\sqrt{x}+2-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\)
\(\sqrt{x}+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(\dfrac{3}{\sqrt{x}+1}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{3}{\sqrt{x}+1}>=-3\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{3}{\sqrt{x}+1}+2>=-3+2=-1\forall x\) thỏa mãn ĐKXĐ
=>\(A>=-1\forall x\) thỏa mãn ĐKXĐ
Vậy: \(A_{min}=-1\) khi x=0
i: \(P=A\left(-x+2\sqrt{x}+3\right)\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\cdot\left(-1\right)\cdot\left(x-2\sqrt{x}-3\right)\)
\(=\dfrac{1-2\sqrt{x}}{\sqrt{x}+1}\cdot\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)\)
\(=\left(1-2\sqrt{x}\right)\left(\sqrt{x}-3\right)\)
\(=\sqrt{x}-3-2x+6\sqrt{x}=-2x+7\sqrt{x}-3\)
\(=-2\left(x-\dfrac{7}{2}\sqrt{x}+\dfrac{3}{2}\right)\)
\(=-2\left(x-2\cdot\sqrt{x}\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{1}{16}\right)\)
\(=-2\left(\sqrt{x}-\dfrac{7}{4}\right)^2+\dfrac{1}{8}< =\dfrac{1}{8}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x}-\dfrac{7}{4}=0\)
=>\(\sqrt{x}=\dfrac{7}{4}\)
=>\(x=\dfrac{49}{16}\)
Đúng 1
Bình luận (0)
Cíu...cíu vứi
Xem thêm câu trả lời
Cíu em cíu emmmmmmm
 cíu tui cíu tui
cíu tui cíu tui
1: Xét ΔMNP vuông tại M có MH là đường cao
nên MH^2=HN*HP; MN^2=NH*NP; PM^2=PH*PN
=>MH=căn 3,6*6,4=4,8cm; MN=căn 3,6*10=6cm; PM=căn 6,4*10=8cm
2: MK=8/2=4cm
Xét ΔMNK vuông tại M có tan MNK=MK/MN=4/6=2/3
nên \(\widehat{MNK}\simeq33^041'\)
3: ΔMNK vuông tại M có MF là đường cao
nên NF*NK=NM^2
ΔMNP vuông tại M có MH là đường cao
nên NH*NP=NM^2
=>NF*NK=NH*NP
Đúng 0
Bình luận (0)
cíu tui cíu tui
Đọc tiếp
cíu tui cíu tui ![]()
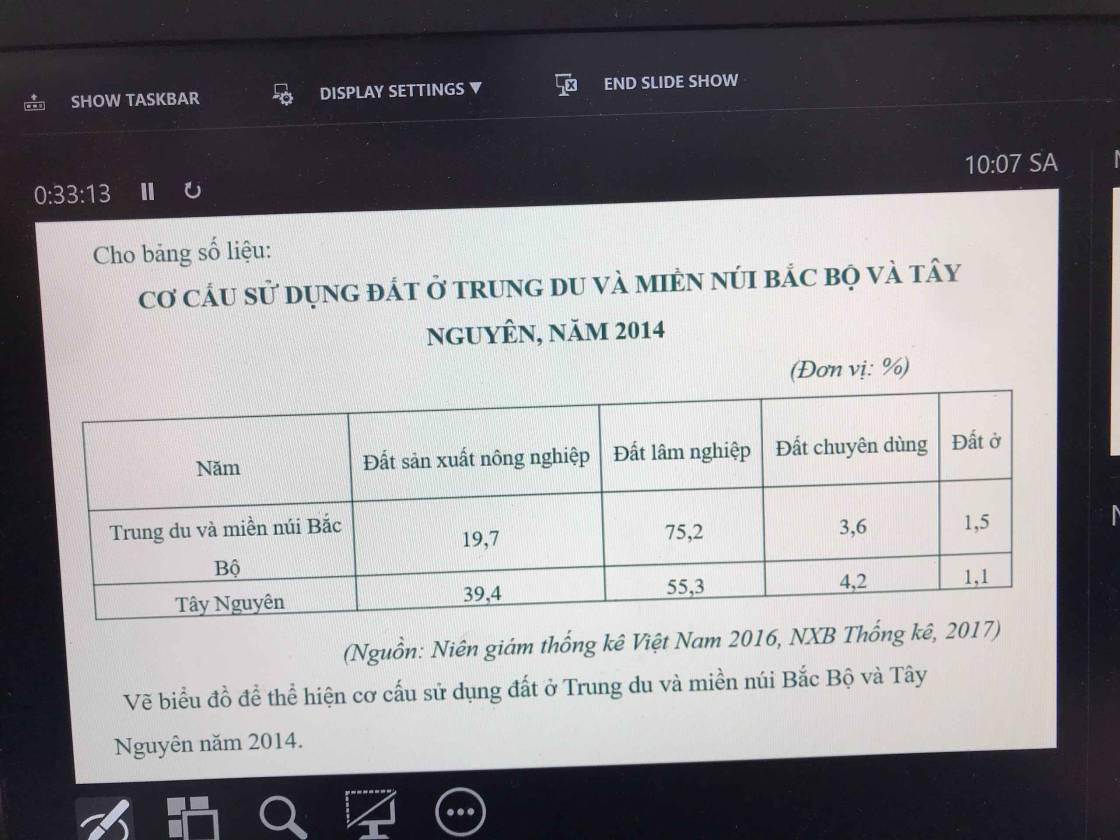

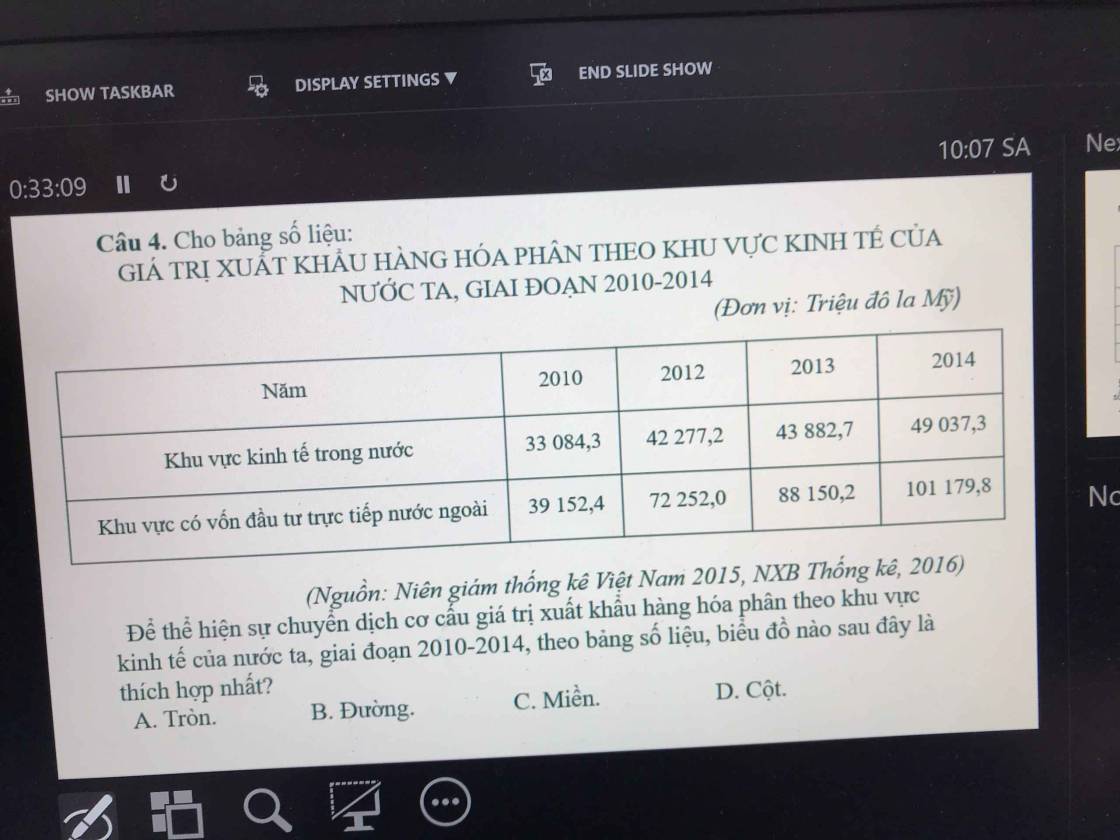

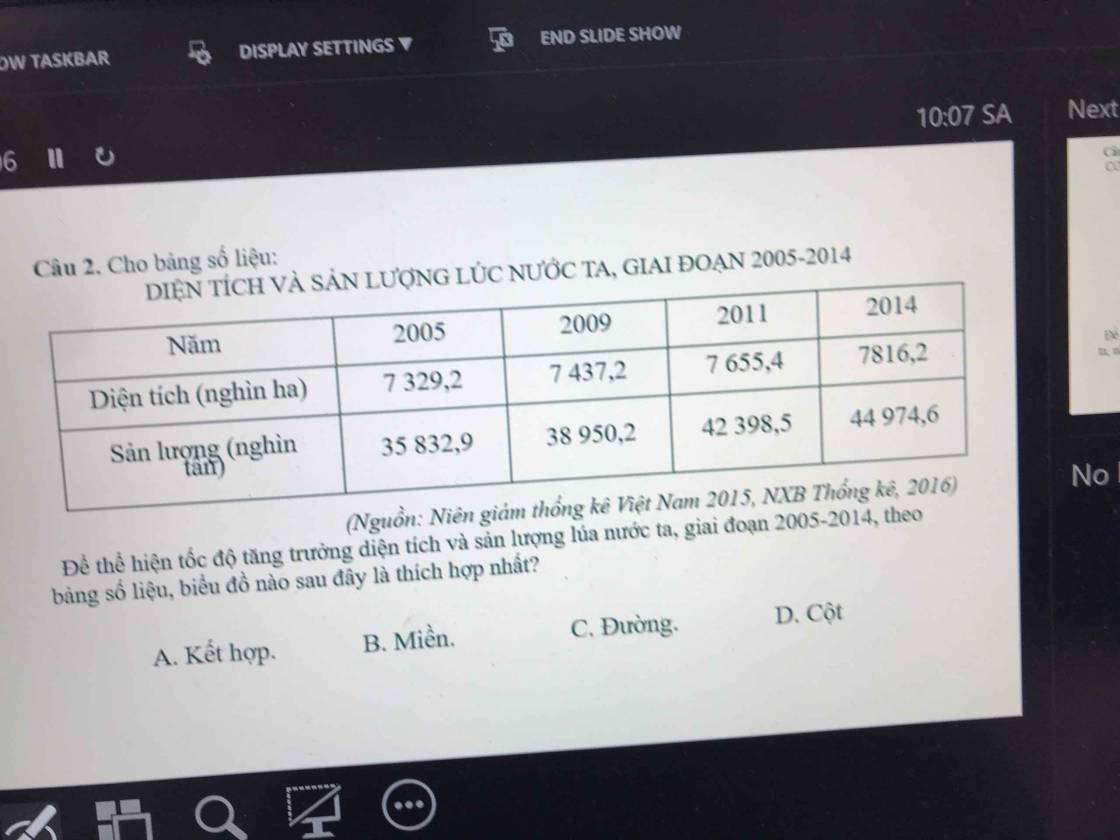
 cíu tui cíu tui
cíu tui cíu tui
a) \(\sqrt[]{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
\(\Leftrightarrow\sqrt[]{3\left(x^2+2x+1\right)+4}+\sqrt{5\left(x^2+2x+1\right)+9}=-\left(x^2+2x+1\right)+5\)
\(\Leftrightarrow\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}=-\left(x+1\right)^2+5\left(1\right)\)
Ta có :
\(\left\{{}\begin{matrix}\sqrt[]{3\left(x+1\right)^2+4}\ge2,\forall x\in R\\\sqrt[]{5\left(x+1\right)^2+9}\ge3,\forall x\in R\end{matrix}\right.\)
\(\Rightarrow VT=\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}\ge5,\forall x\in R\)
\(VP=-\left(x+1\right)^2+5\le5,\forall x\in R\)
Dấu "=" xảy ra thì \(VT=VP=5\)
\(\left(1\right)\Leftrightarrow\left(x+1\right)^2=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Vậy nghiệm của phương trình đã cho là \(x=-1\)
Đúng 0
Bình luận (0)
 cíu tui cíu tui
cíu tui cíu tui
a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot9=36\)
=>\(AH=\sqrt{36}=6\left(cm\right)\)
b: Xét (O) có
ΔAEH nội tiếp
AH là đường kính
Do đó; ΔAEH vuông tại E
=>HE\(\perp\)AE tại E
=>HE\(\perp\)AB tại E
Xét (O) có
ΔAFH nội tiếp
AH là đường kính
Do đó; ΔAFH vuông tại F
=>HF\(\perp\)FA tại F
=>HF\(\perp\)AC tại F
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
c: Ta có: ΔHEB vuông tại E
mà EM là đường trung tuyến
nên EM=HM
=>\(\widehat{MHE}=\widehat{MEH}\)
mà \(\widehat{MHE}=\widehat{ACB}\)(hai góc đồng vị, HE//AC)
nên \(\widehat{MEH}=\widehat{ACB}\)
Ta có: AEHF là hình chữ nhật
=>\(\widehat{FEH}=\widehat{FAH}\)
mà \(\widehat{FAH}=\widehat{ABC}\left(=90^0-\widehat{HCA}\right)\)
nên \(\widehat{FEH}=\widehat{ABC}\)
\(\widehat{MEF}=\widehat{MEH}+\widehat{FEH}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
Vì AEHF là hình chữ nhật
nên AEHF nội tiếp đường tròn đường kính AH và EF
=>EF là đường kính của (O)
Xét (O) có
EF là đường kính
EM\(\perp\)EF tại E
=>EM là tiếp tuyến của (O)
Đúng 1
Bình luận (0)



























