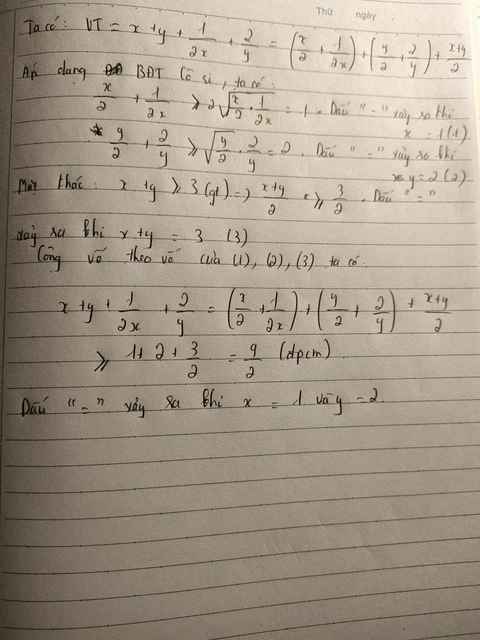Chỗ 3y³ sửa lại thành 3y² nhé!

a) x² -  2xy + y²  + 1 = (x-y)² + 1 \(\ge\)1  

=> (x-y)² +1 >0  =>  x² - 2xy + y²  >0 

b) x - x² - 1 = -(x² - x + \(\frac{1}{4}\)) - \(\frac{3}{4}\)= - (x-\(\frac{1}{2}\))² - \(\frac{3}{4}\)< 0   => x -  x²  - 1 <0

a) Ta có:

\(x^2-2xy+y^2+1\)

\(=\left(x^2-2xy+y^2\right)+1\)

.\(=\left(x-y\right)^2+1\)

\(\left(x-y\right)^2\ge0\)với mọi \(x,y\in R\)

\(\Rightarrow x^2-2xy+y^2+1\)

\(=\left(x-y\right)^2+1\ge0+1=1>0 \forall x,y\in R\left(đpcm\right)\)

b) Ta có :

\(x-x^2-1\)

\(=-\left(x^2-x+1\right)\)

\(=-\left(x^2-2.x.\frac{1}{2}+\frac{1}{2^2}+1-\frac{1}{2^2}\right)\)

\(=-\left[\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\right]\)

Ta có :

\(\left(x-\frac{1}{2}\right)^2\ge0\)với mọi số thực x

\(\Rightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge0+\frac{3}{4}=\frac{3}{4}>0\)với mọi số thực x

\(\Rightarrow x-x^2-1=-\left[\left(x-\frac{1}{2}\right)^2-\frac{3}{4}\right]< 0\)với mọi số thực ( đpcm )

Gọi 3 STN liên tiếp là a;a+1;a+2 Ta có tổng là : a+a+1+a+2=3a+3=3(a+1) số này chia hết cho 3. Tương Tự Gọi 4 STN liên tiếp là a;a+1;a+2;a+3 Ta có: 4a+4=4(a+1) chia hết cho 4

\(B=n^2+\left(n+1\right)^2+n^2\left(n+1\right)^2=n^2\left(n+1\right)^2+\left(2n^2+2n\right)+1=\left[n\left(n+1\right)\right]^2+2n\left(n+1\right)+1\)\(=\left[n\left(n+1\right)+1\right]^2\) là một số chính phương.

1: \(\frac{2x+6}{3x^2-x}:\frac{x^2+3x}{1-3x}\)

\(=\frac{2\left(x+3\right)}{x\left(3x-1\right)}\cdot\frac{-3x+1}{x\left(x+3\right)}\)

\(=\frac{2}{x}\cdot\frac{-\left(3x-1\right)}{x\left(3x-1\right)}=\frac{-2}{x^2}\)

2: \(\frac{x}{x-2y}+\frac{x}{x+2y}+\frac{4xy}{4y^2-x^2}\)

\(=\frac{x}{x-2y}+\frac{x}{x+2y}-\frac{4xy}{\left(x-2y\right)\left(x+2y\right)}\)

\(=\frac{x\left(x+2y\right)+x\left(x-2y\right)-4xy}{\left(x-2y\right)\left(x+2y\right)}=\frac{2x^2-4xy}{\left(x-2y\right)\left(x+2y\right)}\)

\(=\frac{2x\left(x-2y\right)}{\left(x-2y\right)\left(x+2y\right)}=\frac{2x}{x+2y}\)

3: \(\frac{1}{3x-2}-\frac{1}{3x+2}-\frac{3x-6}{4-9x^2}\)

\(=\frac{1}{3x-2}-\frac{1}{3x+2}+\frac{3x-6}{\left(3x-2\right)\left(3x+2\right)}\)

\(=\frac{3x+2-\left(3x-2\right)+3x-6}{\left(3x-2\right)\left(3x+2\right)}=\frac{3x+2-3x+2+3x-6}{\left(3x-2\right)\left(3x+2\right)}\)

\(=\frac{3x-2}{\left(3x-2\right)\left(3x+2\right)}=\frac{1}{3x+2}\)

4: \(\frac{x+3}{x+1}+\frac{2x-1}{x-1}+\frac{x+5}{x^2-1}\)

\(=\frac{x+3}{x+1}+\frac{2x-1}{x-1}+\frac{x+5}{\left(x-1\right)\left(x+1\right)}\)

\(=\frac{\left(x+3\right)\left(x-1\right)+\left(2x-1\right)\left(x+1\right)+x+5}{\left(x-1\right)\left(x+1\right)}\)

\(=\frac{x^2+2x-3+2x^2+2x-x-1+x+5}{\left(x-1\right)\left(x+1\right)}=\frac{3x^2+4x+1}{\left(x-1\right)\left(x+1\right)}\)

\(=\frac{\left(3x+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{3x+1}{x-1}\)

Ta có : \(B=n^2+\left(n+1\right)^2+n^2\left(n+1\right)^2=n^2\left(n+1\right)^2+\left(2n^2+2n\right)+1=n^2\left(n+1\right)^2+2n\left(n+1\right)+1\)

\(=\left[n\left(n+1\right)+1\right]^2\) là một số chính phương.

Bạn thêm điều kiện n là số tự nhiên nhé ^^