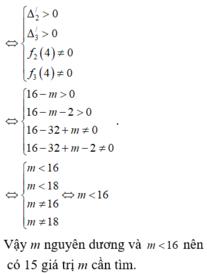Số các giá trị nguyên dương của m để y=3x-2m+2 dương với mọi x thuộc [18:21]

Những câu hỏi liên quan
Giúp mik giải bài này với ạ
Cho hàm số f(x)= x^2 - 2mx +2m -1 (m là tham số). Có bao nhiêu giá trị nguyên của m thuộc (-10;10) để f(x) dương với mọi x thuộc (3; +∞)
Cho hàm số
f
(
x
)
m
-
2
x
3
-
2
2
m
-
3
x
2
+
5
m
-
3
x...
Đọc tiếp
Cho hàm số f ( x ) = m - 2 x 3 - 2 2 m - 3 x 2 + 5 m - 3 x - 2 m - 2 với m là tham số thực. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f x có 5 điểm cực trị?
A. 0.
B. 3.
C. 2.
D. 1.
Hàm số y = f x với f(x) là hàm đa thức bậc 3 có 5 điểm cực trị khi và chỉ khi hàm số f(x) có hai cực trị và đồ thị của hàm số cắt trục hoành tại 3 điểm phân biệt.
Mặt khác, f(x) là hàm số bậc 3 nên khi đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt thì hàm số đồng thời cũng có hai cực trị. Do đó ta chỉ cần tìm điều kiện để phương trình f(x) = 0 có 3 nghiệm phân biệt.

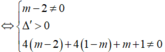
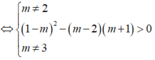
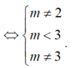

Chọn D
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm
f
(
x
)
(
x
-
1
)
2
(
x
2
-
2
x
)
với mọi x thuộc R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
y
f
(
x
2
-...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x 2 - 2 x ) với mọi x thuộc R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x 2 - 8 x + m ) có 5 điểm cực trị?
A. 15
B. 17
C. 16.
D. 18
Tìm các giá trị của tham số m để tam thức bậc hai sau dương với mọi \(x \in \mathbb{R}\):
\({x^2} + (m + 1)x + 2m + 3\)
Để tam thức bậc hai \({x^2} + (m + 1)x + 2m + 3 > 0\)với mọi \(x \in \mathbb{R}\)
Ta có: a = 1 >0 nên \(\Delta < 0\)
\(\begin{array}{l} \Leftrightarrow {(m + 1)^2} - 4.(2m + 3) < 0\\ \Leftrightarrow {m^2} + 2m + 1 - 8m - 12 < 0\\ \Leftrightarrow {m^2} - 6m - 11 < 0\end{array}\)
Tam thức \(f(m) = {m^2} - 6m - 11\) có \(\Delta ' = 20 > 0\) nên f(x) có 2 nghiệm phân biệt \({m_1} = 3+\sqrt{20}; {m_2} = 3-\sqrt{20}\)
Khi đó
\( 3+\sqrt{20} < m < 3-\sqrt{20}\)
Vậy \( 3+\sqrt{20} < m < 3-\sqrt{20}\)
Đúng 0
Bình luận (0)
Cho M = 5ax^2y^2 + (-1/2ax^2y^2) + 7ax^2y^2 + (-x^2y^2)
a) Với giá trị nào của a thì M không âm với mọi x, y
b) Với giá trị nào của a thì M không dương với mọi x, y
c) Cho a =2 . Tìm các cặp số nguyên (x; y) để M = 84
a: M=x^2y^2(5a-1/2a+7a-1)
=(23/2a-1)*x^2y^2
M>=0
=>23/2a-1>=0
=>23/2a>=1
=>a>=2/23
b: M<=0
=>23/2a-1<=0
=>a<=2/23
c: a=2 thì M=22x^2y^2
M=84
=>x^2y^2=84/22=42/11
mà x,y nguyên
nên \(\left(x,y\right)\in\varnothing\)
Đúng 0
Bình luận (0)
Cho M = 5ax^2y^2 + (-1/2ax^2y^2) + 7ax^2y^2 + (-x^2y^2)
a) Với giá trị nào của a thì M không âm với mọi x, y
b) Với giá trị nào của a thì M không dương với mọi x, y
c) Cho a =2 . Tìm các cặp số nguyên (x; y) để M = 88
M = 5x^2y^2+(-1/2ax^2y^2)+7ax^2+(-x^2y^2)
M=(5a+(-1/2a)+7a+(-1)) . x^2y^2
M= (23/2a - 1) x^2y^2
a)voi gia tri nao cua a thi M ko am
⇒M ≥ 0 ⇒(23/2a - 1).x^2y^2 ≥0
⇒23/2a - 1 ≥ 0 vi x^2y^2 ⇒0 ∀ x;y
⇒23/2a ≥ 0
⇒a ≥ . 2/23
⇒a ≥ 2/23
Vay a ≥ 2/23 thi M ko am voi moi x;y
b)Voi gia tri nao cua a thi M ko dg
⇒M ≤ 0 ⇒ (23/2a - 1).x^2y^2 ≤ 0 ∀ x.y
⇒23/2a ≤ 1
⇒ a ≤ 2/23
Voi moi a ≤2/23 thi M ko duong voi moi x;y
c) Thay a=2 vao M ta dc:
M= (23.2:2 -1).x^2y^2
M=22x^2y^2
De M=88 ⇒22x^2y^2 =88 ⇒x^2y^2=4
⇒(xy^2)= 2^2 ⇒ xy=2
⇒x= 2⇒y=1 ; x=1⇒y=2 ; x=-2 ⇒y=-1 ; x=-1y⇒-2
Vay(x;y)= ( (2;1); (1;2); (-2;-1); (-1;-2) thi M = 88
(ko danh dc dau cua chu ban thong cam cho mik)
Đúng 1
Bình luận (0)
a) Tìm tất cả các tham số m nguyên để \(F\left(x\right)=\dfrac{7}{x^2+\dfrac{1}{2}m}\) có nghiệm x nguyên và F(x) là số nguyên dương.
b) Với mọi \(m\ge0\), tìm giá trị lớn nhất của F(x).
Với mọi m < 0, tìm giá trị nhỏ nhất của F(x).
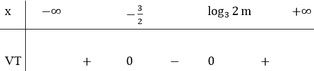
Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình
(
3
x
+
2
-
3
)
(
3
x
-
2
m
)
0
chứa không quá 9 số nguyên? A. 3281. B. 3283. C. 3280. D. 3279.
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình ( 3 x + 2 - 3 ) ( 3 x - 2 m ) < 0 chứa không quá 9 số nguyên?
A. 3281.
B. 3283.
C. 3280.
D. 3279.
Tính tổng:
M = 5ax^2y^2 + (-1/2ax^2y^2) + 7ax^2y^2 + (-x^2y^2)
a) Với giá trị nào của a thì M không âm với mọi x, y
b) Với giá trị nào của a thì M không dương với mọi x, y
c) Cho a = . Tìm các cặp số nguyên (x; y) để M = 84
M=5ax2y2+(-1/22y2)+7ax2y2+(-x2y2)
M=[5a+(-1/2a)+7a+(-1)]x2y2
M=(23/2a-1)x2y2
a; Nếu M không âm với mọi x, y thì (23/2a-1) phải lớn hơn hoặc bằng 0 hay a lớn hơn hoặc bằng 23/2
b; Tương tự thì (23/2a-1) phải bé hơn hoặc bằng 0 hay a bé hơn hoặc bằng 23/2
Đúng 0
Bình luận (0)