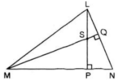
a/ Chứng minh NS vuông góc LM.
b/ Khi góc LMP = 50o, hãy tính góc MSP và góc PSQ.
Cho hình 57.
Khi góc LNP = 50o, hãy tính góc MSP và góc PSQ.
Hình 57
+ Ta có : trong tam giác vuông, hai góc nhọn phụ nhau nên :
ΔNMQ vuông tại Q có:

Cho hình 57 :
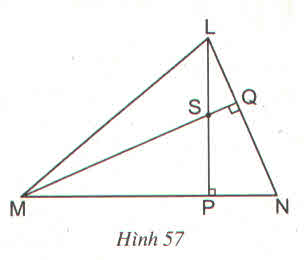
a) Chứng minh \(NS\perp LM\)
b) Khi \(\widehat{LNP}=50^0\), hãy tính góc MSP và góc PSQ
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay SN ⊥ ML
Cho hình dưới
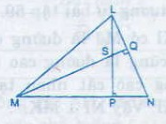
a) Chứng minh NS ⊥ LM
b) Khi =500, hãy tính góc MSP và góc PSQ
a) Chứng minh NS ⊥ LM
b) Khi =500, hãy tính góc MSP và góc PSQ
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có =500 nên
=400
∆MPS vuông tại Q có =400 nên
=500
Suy ra =1300(kề bù)
Cho tam giác ABC . Hai đường cao BM và CN cắt nhau tại H.
a. Chứng minh rằng AH vuông góc BC.
b. Khi góc BAC = 70 độ . Hãy tính góc BHNvà góc MHN.
c. Khi góc ACB = 50 độ . Hãy tính góc AHM.
a: XétΔABC có
BM là đường cao
CN là đường cao
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
Suy ra: AH vuông góc với BC
b: \(\widehat{MHN}=360^0-90^0-90^0-70^0=110^0\)
=>\(\widehat{BHN}=70^0\)
Cho AB // EG và một điểm C bất kì như hình vẽ và A = 40o ; E = 50o. Chứng minh rằng AC vuông góc với CE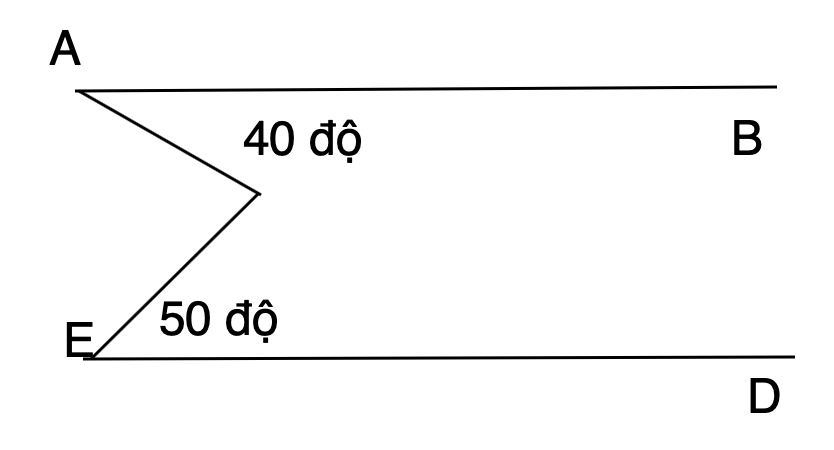
Kẻ 1 đường thẳng t qua C song song với AB và ED.
=> \(\widehat{tCA}=\widehat{A}=40^o\) (so le trong)
\(\widehat{tCE}=\widehat{E}=50^o\) (so le trong)
Ta có: \(\widehat{C}=40^o+50^o=90^o\)
=> \(AC\perp CE\)
Cho tam giác ABC vuông tại A. Trên cạnh AB lấy điểm E, kẻ EF vuông góc với BC (F thuộc BC) gọi K là giao điểm của hai đường thẳng EF và AC a. Chứng minh rằng CE vuông góc BK b. Khi góc ACB bằng 50 độ hãy tính số đo góc AEF cú tuôiii dới 😭
a: Xét ΔCKB có
KF là đường cao
BA là đường cao
KF cắt BA tại E
DO đó: CE⊥BK
b: \(\widehat{AEF}=180^0-50^0=130^0\)
Cho tam giác DEF có DE = DF. Gọi K là trung điểm của EF.
a) Chứng minh: ∆ = ∆ DEK DFK .
b) Chứng minh: DK là tia phân giác của góc EDF.
c) Giả sử 50o E = . Tính số đo góc F và góc EDF?
a: Xét ΔDEK và ΔDFK có
DE=DF
EK=FK
DK chung
Do đó: ΔDEK=ΔDFK
b: Ta có: ΔDEF cân tại D
mà DK là đường trung tuyến
nên DK là đường phân giác
c: \(\widehat{F}=\widehat{E}=50^0\)
\(\widehat{EDF}=180^0-2\cdot50^0=80^0\)
Hãy vẽ hình, biết zz' vuông góc với xx' và zz' vuông góc với yy' . Tia Bm là tia phân giác của góc ABy'
a) Chứng minh xx' song song với yy'
b) Tính góc mCx'
c) Chứng minh góc ABC bằng góc ACB
1. cho tam giác ABC vuông tại A.
* cho góc B bằng 50o , tính số đo góc C
*trên 2 tia đối của tia CA lấy điểm D sao cho C là chung điểm của AD . qua D kẻ đường thẳng vuông góc với AD cắt đường thẳng BC tại E
a, chứng minh : CB =CE
b, qua c kẻ đường thẳng vuông góc với BE cắt đường thẳng ED tại I . chứng minh : BI=AB+DI
2.tìm 3 số ABC biết : 3a-2b / 5 = 2c-5a / 3= 5b-3c / 2 và a2+ 275 =bc
Thu gọn