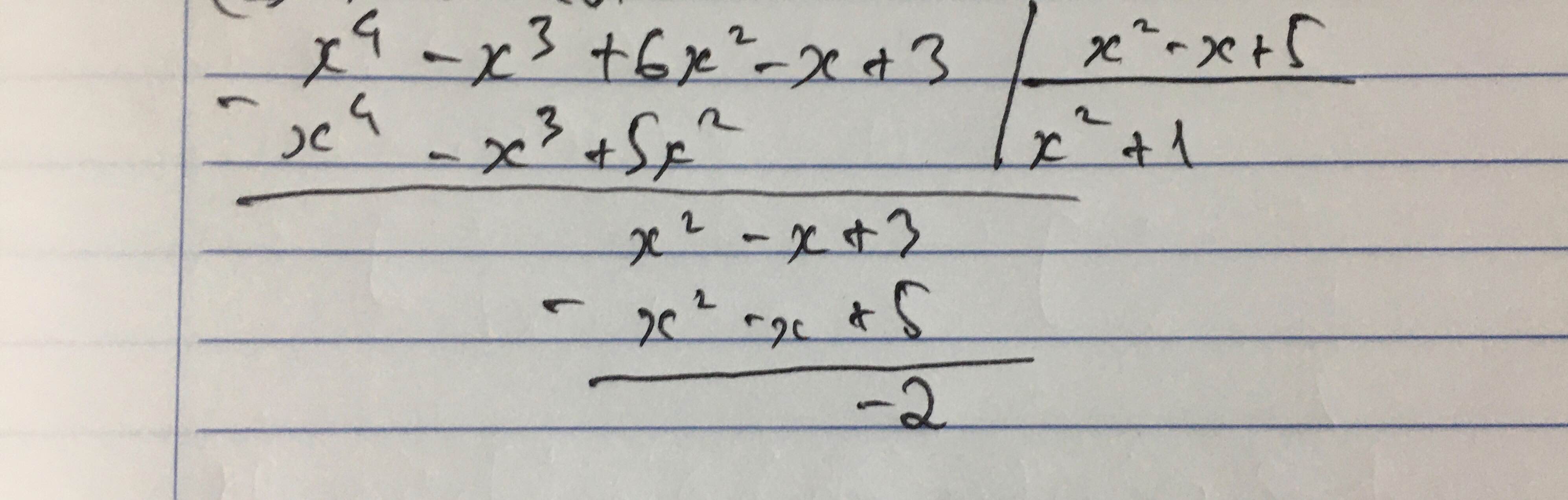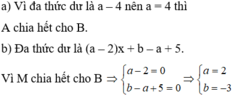chia đa thức x4 – x3 + x2 + 3x cho đa thức x2 – 2x + 3

Những câu hỏi liên quan
x4-x3-3x2+ax +b chia cho đa thức x2-x-2 dư 2x-3
dựa vào đây nha bạn: https://hoc24.vn/hoi-dap/question/476806.html
Vậy \(a=3;b=-1.\)
Chúc bạn học tốt!
Cho đa thức
F(x)=x5 - 3x2 -x3 - x2 - 2x + 5
G(x)+x5 - x4 + x2 - 3x + x2 + 1
Tính H(x) = F(x) + G(x)
\(H\left(x\right)=F\left(x\right)+G\left(x\right)=\left(x^5-3x^2-x^3-x^2-2x+5\right)+\left(x^5-x^4+x^2-3x+x^2+1\right)\\ =x^5-3x^2-x^3-x^2-2x+5+x^5-x^4+x^2-3x+x^2+1\\ =\left(x^5+x^5\right)-x^4-x^3-\left(3x^2+x^2-x^2-x^2\right)-\left(2x+3x\right)+5\\ =2x^5-x^4-x^3-2x^2-5x+5\)
Đúng 0
Bình luận (0)
Cho đa thức A = x4 + x3 – 2x – 2
a) Tìm đa thức B sao cho A + B = x3 + 3x + 1
b) Tìm đa thức C sao cho A – C = x5
c) Tìm đa thức D biết rằng D = (2x2 – 3) . A
d) Tìm đa thức P sao cho A = (x+1) . P
e) Có hay không một đa thức Q sao cho A = (x2 + 1) . Q?
a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
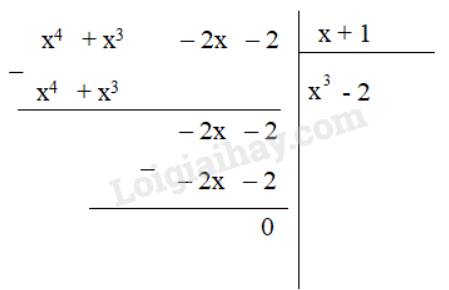
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
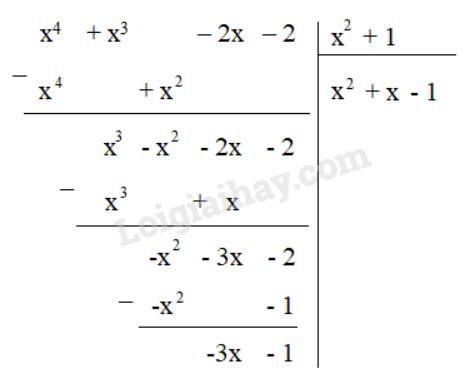
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn
Đúng 1
Bình luận (0)
Chia đa thức cho đa thức: (mình cần gấppppppp
(x4-x3+6x2-x+3) : (x2-x+5)
Ta có: \(\dfrac{x^4-x^3+6x^2-x+3}{x^2-x+5}\)
\(=\dfrac{x^4-x^3+5x^2+x^2-x+5-2}{x^2-x+5}\)
\(=x^2+1-\dfrac{2}{x^2-x+5}\)
Đúng 0
Bình luận (0)
Đa thức x3-3x+a chia hết cho đa thức x2-2x+1
Answer:
Gọi thương của phép chia là \(P\left(x\right)\)
\(x^3-3x+a\)
\(=\left(x^2-2x+1\right).P\left(x\right)\forall x\)
\(\Leftrightarrow x^3-3x+a\)
\(=\left(x-1\right)^2.P\left(x\right)\forall x\)
Với \(x=1\) (Để cho \(\left(x-1\right)^2=0\))
\(\Rightarrow1^3-3.1+a=0\)
\(\Rightarrow1-3+a=0\)
\(\Rightarrow a=2\)
Cho các đa thức f(x) = x5 – 3x2 + x3 – x2 - 2x + 5
g(x) = x5 – x4 + x2 - 3x + x2 + 1
a) Thu gọn và sắp xếp đa thức f(x) và g(x) theo luỹ thừa giảm dần.
b)Tính h(x) = f(x) + g(x)
a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
Đúng 1
Bình luận (0)
Tìm a và b để đa thức A chia hết cho đa thức B với:a) A
x
3
-
9
x
2
+17x - 25 + a và B
x
2
- 2x + 3;b) A
x
4
-
7
x
3
+
10
x
2
+(a - 1)x + b...
Đọc tiếp
Tìm a và b để đa thức A chia hết cho đa thức B với:
a) A = x 3 - 9 x 2 +17x - 25 + a và B = x 2 - 2x + 3;
b) A = x 4 - 7 x 3 + 10 x 2 +(a - 1)x + b - a và B = x 2 -6x + 5.
cho hai đa thức :A=x5 -3x3+x2-x3-3+2x;B=x4-3x-2+5x2-3x4+2x5 a)sắp xếp đa thức A và B theo luỹ thừa của biến b) tính A+B, A-
a. \(A=x^5-3x^3+x^2-x^3-3+2x=x^5-4x^3+x^2+2x-3\)
\(B=x^4-3x-2+5x^2-3x^4+2x^5=2x^5-2x^4+5x^2-3x-2\)
b. \(A+B=x^5-4x^3+x^2+2x-3+2x^5-2x^4+5x^2-3x-2\)
\(=3x^5-2x^4-4x^3+6x^2-x-5\)
Đúng 2
Bình luận (0)
Bài 3 : (2 điểm) Cho hai đa thức : A(x) = 2 x3 + 5 + x2 –3 x –5x3 –4
B(x) = –3x4 – x3 + 2x2 + 2x + x4 – 4–x2 .
a) Thu gọn 2 đa thức trên.
b) Tính H(x) = A(x) – B(x)
a) A(x) = 2x3 + 5 + x2 - 3x - 5x3 - 4
= 2x3 - 5x3 + x2 - 3x + 5 - 4
= -3x3 + x2 - 3x + 1
B(x) = -3x4 - x3 + 2x2 + 2x + x4 - 4 - x2
= -3x4 + x4 - x3 + 2x2 - x2 + 2x - 4
= -2x4 - x3 + x2 + 2x - 4
b)
H(x) = A(x) - B(x)
H(x) = (-3x3 + x2 - 3x + 1) - (-2x4 - x3 + x2 + 2x - 4)
= -3x3 + x2 - 3x + 1 + 2x4 + x3 - x2 - 2x + 4
= 2x4 - 3x3 + x3 + x2 - x2 - 3x - 2x + 1 + 4
= 2x4 - 2x3 -5x + 5
Đúng 1
Bình luận (0)
a) A(x)=(2x3-5x3) +(5-4) + x2- 3x
=-3x3+1+x2-3x
B(x)=(-3x4+x4) - x3+(2x2-x2) +2x - 4
=-2x4-x3+x2+2x - 4
b) A(x) - B(x) = (-3x3+1+x2-3x) - (-2x4-x3+x2+2x - 4)
= -3x3+1+x2-3x - 2x4+x3-x2-2x + 4
=(-3x3+x3) + (1+4) + (+x2-x2) + (-3x-2x) - 2x4
=-2x3 + 5 - 5x -2x4
Đúng 0
Bình luận (0)