giúp mình bài 1 câu a với ạ

giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Giúp mình bài 1 câu a và hết bài 2 với ạ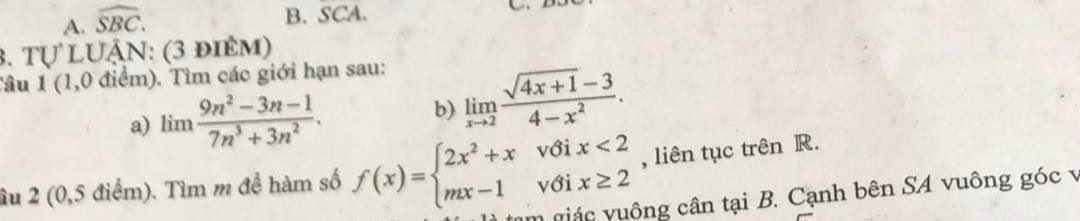
Câu 1 : a . \(lim\dfrac{9n^2-3n-1}{7n^3+3n^2}=lim\dfrac{\dfrac{9}{n}-\dfrac{3}{n^2}-\dfrac{1}{n^3}}{7+\dfrac{3}{n}}=0\)
b. \(lim_{x\rightarrow2}\dfrac{\sqrt{4x+1}-3}{4-x^2}=lim_{x\rightarrow2}\dfrac{4x+1-9}{\left(\sqrt{4x+1}+3\right)\left(4-x^2\right)}\)
\(=lim_{x\rightarrow2}\dfrac{4\left(x-2\right)}{\left(\sqrt{4x+1}+3\right)\left(2-x\right)\left(2+x\right)}\)
\(=lim_{x\rightarrow2}\dfrac{-4}{\left(\sqrt{4x+1}+3\right)\left(2+x\right)}=\dfrac{-4}{\left(3+3\right)\left(2+2\right)}=-\dfrac{1}{6}\)
Câu 2 : Ta có : f(x) = \(\left\{{}\begin{matrix}2x^2+x\left(x< 2\right)\\mx-1\left(x\ge2\right)\end{matrix}\right.\)
TXĐ : D = R . Với x < 2 ; hàm số liên tục
Với x > 2 ; hàm số liên tục
Với x = 2 , ta có : \(lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^-}2x^2+x=2.2^2+2=10\)
\(lim_{x\rightarrow2^+}f\left(x\right)=lim_{x\rightarrow2^+}mx-1=2m-1\)
Hàm số liên tục trên R <=> Hàm số liên tục tại x = 2
\(\Leftrightarrow lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^+}f\left(x\right)\)
\(\Leftrightarrow10=2m-1\) \(\Leftrightarrow m=\dfrac{11}{2}\)
Vậy ...
 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
Dạ mng xem giúp mình mấy bài trắc nghiệm làm đúng chưa với ạ , mng giúp mình luôn câu 5 bài 2 và câu 2 bài 3 ạ
Mình cảm ơn trước ạ


Bài 2
5 C
Bài 3
1 D
6 C
Còn lại ol r nhé
giúp mình câu c bài 1 và cả bài 2 với ạ
Bài 1:
a: Xét tứ giác BEDF có
ED//BF
ED=BF
Do đó: BEDF là hình bình hành
Suy ra: BE=DF
c: ta có: BEDF là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường
mà AC và BD cắt nhau tại trung điểm của mỗi đường
nên AC,BD,EF đồng quy
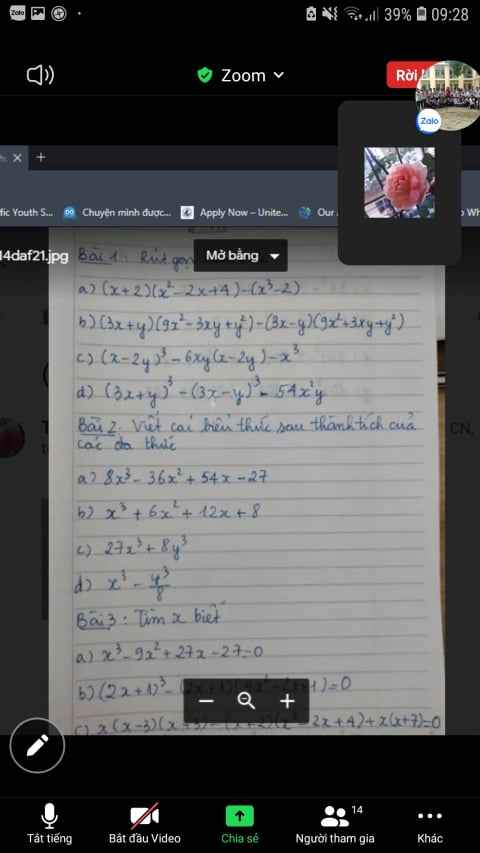
làm giúp mình bài 2 với câu d bài 1 vs ạ
Bài 2:
a: \(8x^3-36x^2+54x-27=\left(2x-3\right)^3\)
b: \(x^3+6x^2+12x+8=\left(x+2\right)^3\)
c: \(27x^3+8y^3=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)\)
d: \(x^3-\dfrac{y^3}{8}=\left(x-\dfrac{1}{2}y\right)\left(x^2+\dfrac{1}{2}xy+\dfrac{1}{4}y^2\right)\)
giúp mình bài 1 câu g,h và bài 2 với ạ
Làm giúp mình 5 câu cuối bài 1 và bài 2 với ạ

6) \(\dfrac{8^6}{256}=\dfrac{\left(2^3\right)^6}{2^8}=\dfrac{2^{18}}{2^8}=2^{10}=1024\)
7) \(\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{4}\right)^{20}=\left(\dfrac{1}{2}\right)^{15}.\left[\left(\dfrac{1}{2}\right)^2\right]^{20}=\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{2}\right)^{40}=\left(\dfrac{1}{2}\right)^{55}=\dfrac{1}{2^{55}}\)
8) \(\left(\dfrac{1}{9}\right)^{25}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{50}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{20}=\dfrac{1}{3^{20}}\)
9)\(\left(\dfrac{1}{16}\right)^3\div\left(\dfrac{1}{8}\right)^2=\left(\dfrac{1}{2}\right)^{12}\div\left(\dfrac{1}{2}\right)^6=\left(\dfrac{1}{2}\right)^6=\dfrac{1}{64}\)
10) \(\dfrac{27^2.8^5}{6^2.32^3}=\dfrac{3^6.2^{15}}{3^2.2^2.2^{15}}=\dfrac{3^4}{2^2}=\dfrac{81}{4}\)
Mọi người giúp mình bài 8 và bài 9 câu a với ạ 
8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)