Vì : \(\frac{AC}{BD}=1,05\)

\(\Rightarrow\frac{\frac{1}{2}AC}{\frac{1}{2}BD}=1,05\)

\(\Rightarrow\frac{AO}{BO}=1,05\)

\(\Rightarrow AO=1,05.BO\)

Xét \(\Delta AOB\) vuông tại O ( vì O là giao điểm 2 đường chéo của hình thoi )

\(AO^2+BO^2=AB^2\) ( định lí Py ta go )

\(\left(1,05.BO\right)^2+BO^2=58^2\)

\(2,1025BO^2=3364\)

\(\Rightarrow BO^2=1600\)

\(\Rightarrow BO=40\) ( vì \(BO>0\) )

\(\Rightarrow AC=\left(BO.1,05\right).1=84\left(cm\right)\)

Vậy ..............

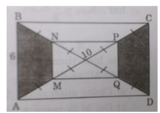
a) Ta có MN và PQ lần lượt là các đường trung bình của các tam giác AOB và COD mà AB // CD và AB = CD nên MN // PQ và MN = PQ

⇒ Tứ giác MNPQ là hình bình hành.

Tương tự NP // BC mà AB ⊥ BC nên MN ⊥ NP. Do đó MNPQ là hình chữ nhật.

Trong ΔABC ta có

Vậy SMNPQ = MN.PQ = 3.4 = 12 (cm2).

b)Dễ thấy ΔAOB = ΔCOD (c.c.c).

Tương tự ΔMON = ΔPOQ

Do đó: SAOB = SCOD và SMON = SPOQ.

⇒ SAOB - SMON = SCOD - SPOQ hay SAMNB = SCPQD.

Tứ giác ABCD là một hình vuông.

OA=5cm

OA=5cm

Vì \(\frac{AC}{BD}=1,05\)

\(\Rightarrow\frac{\frac{1}{2}AC}{\frac{1}{2}BD}=1,05\)

\(\Rightarrow\frac{AO}{BO}=1,05\)

\(\Rightarrow AO=1,05.BO\)

Xét \(\Delta AOB\)vuông tại O ( vì O là giao điểm 2 đường chéo hình thoi ) có :

\(AO^2+BO^2=AB^2\)( Định lý Pytago )

\(\left(1,05.BO\right)^2+BO^2=58^2\)

\(2,1025BO^2=3364\)

\(\Rightarrow BO^2=1600\)

\(\Rightarrow BO=40\) \(\left(BO>0\right)\)

\(\Rightarrow AC=\left(BO.1,05\right).2=84\)(cm)

Vậy ...

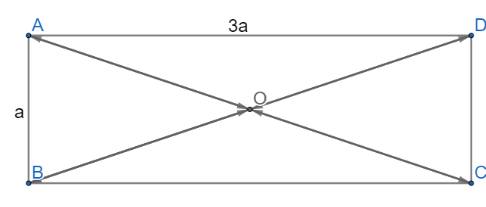
a) Ta có:

\(AC = BD = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{a^2} + {{\left( {3a} \right)}^2}}  = a\sqrt {10} \)

+) \(\left| {\overrightarrow {AC} } \right| = AC = a\sqrt {10} \)

+) \(\left| {\overrightarrow {BD} } \right| = BD = a\sqrt {10} \)

b) O là giao điểm của hai đường chéo nên ta có:

\(AO = OC = BO = OD = \frac{{a\sqrt {10} }}{2}\)

Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng

Suy ra các cặp vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt {10} }}{2}\) là:

\(\overrightarrow {OA} \) và \(\overrightarrow {OC} \); \(\overrightarrow {AO} \) và \(\overrightarrow {CO} \); \(\overrightarrow {OB} \) và \(\overrightarrow {OD} \); \(\overrightarrow {BO} \) và \(\overrightarrow {DO} \)