Giá trị của x thỏa mãn biểu thức −2.(x−5)>0là

Những câu hỏi liên quan
Cho các số nguyên x,y thỏa mãn 5x - 2y =1. Tìm giá trị nhỏ nhất của biểu thức \(T=3|x|+5|y|\)
Cho các số nguyên x,y thỏa mãn 5x-2y=1. Tìm giá trị nhỏ nhất của biểu thức \(T=3|x|+5|y|\)
bạn ơi. Bạn có đáp án của bài này chưa vậy. Cho mik xin vs
mik đang cần gấp
Đúng 0
Bình luận (0)
Cho
z
x
+
y
i
với x, y
∈
R
là số phức thỏa mãn điều kiện
z
¯
+
2
-
3
i
≤
|
z
+
i
-
2
|
≤
5
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ...
Đọc tiếp
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
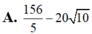
![]()
![]()
Cho các số thực x, y thỏa mãn
x
+
y
2
x
-
3
+
y
+
3
. Giá trị nhỏ nhất của biểu thức
P
4
(
x
2
+
y
2
)
+
15
x...
Đọc tiếp
Cho các số thực x, y thỏa mãn x + y = 2 x - 3 + y + 3 . Giá trị nhỏ nhất của biểu thức P = 4 ( x 2 + y 2 ) + 15 x y là:
A. minP = -83
B. minP = -63
C. minP = -80
D. minP = -91
Xét các số thực dương a, thỏa mãn a+b=1 . Tìm giá trị nhỏ nhất của biểu thức P=a^2 +b
\(a+b=1\Leftrightarrow b=1-a\\ \Leftrightarrow P=a^2+1-a=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ P_{min}=\dfrac{3}{4}\Leftrightarrow a=\dfrac{1}{2}\Leftrightarrow b=\dfrac{1}{2}\)
Đúng 3
Bình luận (0)
Cho các số x,y,z thỏa mãn : x^2+y^2+z^2=xy+yz+zx và x^2018 +y^2018+z^2018=3. Tính giá trị của biểu thức P=x^28+y^57+z^2017
Cho số thực x thỏa mãn \(^{x^2-4x+1=0}\)Tính giá trị của biểu thức \(G=\frac{x^2}{x^4+1}\)
\(x^2-4x+1=0\)
( a = 1 ; b = -4 ; c =1 )
\(\Delta=b^2-4ac\)
\(=\left(-4\right)^2-4.1.1\)
\(=16-4\)
\(=12>0\)
\(\sqrt{\Delta}=\sqrt{12}=2\sqrt{3}\)
Vì \(\Delta>0\) nên phương trình có 2 nghiệm phân biệt
\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{4+2\sqrt{3}}{2.1}=2+\sqrt{3}\)
\(x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{4-2\sqrt{3}}{2.1}=2-\sqrt{3}\)
Ta có : \(G=\frac{x^2}{x^4+1}\)
. Thay \(x_1\) vào ta được : \(G=\frac{\left(2+\sqrt{3}\right)^2}{\left(2+\sqrt{3}\right)^4+1}\)
\(=\frac{4+4\sqrt{3}+3}{\left(4+4\sqrt{3}+3\right)^2+1}\)
\(=\frac{4\sqrt{3}+7}{\left(4\sqrt{3}+7\right)^2+1}\)
\(=\frac{4\sqrt{3}+7}{48+56\sqrt{3}+49+1}\)
\(=\frac{4\sqrt{3}+7}{56\sqrt{3}+98}\)
\(=\frac{4\sqrt{3}+7}{14.\left(4\sqrt{3}+7\right)}\)
\(=\frac{1}{14}\)
.Thay \(x_2\) vào ta được : \(G=\frac{\left(2-\sqrt{3}\right)^2}{\left(2-\sqrt{3}\right)^4+1}\)
\(=\frac{4-4\sqrt{3}+3}{\left(4-4\sqrt{3}+3\right)^2+1}\)
\(=\frac{7-4\sqrt{3}}{\left(7-4\sqrt{3}\right)^2+1}\)
\(=\frac{7-4\sqrt{3}}{49-56\sqrt{3}+48+1}\)
\(=\frac{7-4\sqrt{3}}{98-56\sqrt{3}}\)
\(=\frac{7-4\sqrt{3}}{14.\left(7-4\sqrt{3}\right)}=\frac{1}{14}\)
Vậy giá trị của biểu thức là 1/14
Đúng 0
Bình luận (0)
a) Cho x+y=1. Tìm giá trị nhỏ nhất của biểu thức x3+y3
b) Cho 3 số dương x, y, z thỏa mãn điều kiện x+y+z=2. Tìm GTNN của biểu thức: P=\(\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{y+x}\)
a, Từ x+y=1
=>x=1-y
Ta có: \(x^3+y^3=\left(1-y\right)^3+y^3=1-3y+3y^2-y^3+y^3\)
\(=3y^2-3y+1=3\left(y^2-y+\frac{1}{3}\right)=3\left(y^2-2.y.\frac{1}{2}+\frac{1}{4}+\frac{1}{12}\right)\)
\(=3\left[\left(y-\frac{1}{2}\right)^2+\frac{1}{12}\right]=3\left(y-\frac{1}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}\) với mọi y
=>GTNN của x3+y3 là 1/4
Dấu "=" xảy ra \(< =>\left(y-\frac{1}{2}\right)^2=0< =>y=\frac{1}{2}< =>x=y=\frac{1}{2}\) (vì x=1-y)
Vậy .......................................
b) Ta có: \(P=\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{y+x}\)
\(=\left(\frac{x^2}{y+z}+x\right)+\left(\frac{y^2}{z+x}+y\right)+\left(\frac{z^2}{y+z}+z\right)-\left(x+y+z\right)\)
\(=\frac{x\left(x+y+z\right)}{y+z}+\frac{y\left(x+y+z\right)}{z+x}+\frac{z\left(x+y+z\right)}{y+z}-\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{y+x}-1\right)\)
Đặt \(A=\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{y+x}\)
\(A=\left(\frac{x}{y+z}+1\right)+\left(\frac{y}{z+x}+1\right)+\left(\frac{z}{y+x}+1\right)-3\)
\(=\frac{x+y+z}{y+z}+\frac{x+y+z}{z+x}+\frac{x+y+z}{y+x}-3\)
\(=\left(x+y+z\right)\left(\frac{1}{y+x}+\frac{1}{y+z}+\frac{1}{z+x}\right)-3\)
\(=\frac{1}{2}\left[\left(x+y\right)+\left(y+z\right)+\left(z+x\right)\right]\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)-3\ge\frac{9}{2}-3=\frac{3}{2}\)
(phần này nhân phá ngoặc rồi dùng biến đổi tương đương)
\(=>P=\left(x+y+z\right)\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{y+x}-1\right)\ge2\left(\frac{3}{2}-1\right)=1\)
=>minP=1
Dấu "=" xảy ra <=>x=y=z
Vậy.....................
Đúng 0
Bình luận (0)
a) Cho 3 số không âm x, y, z thỏa mãn: x^2+y^2+z^21.Tìm giá trị nhỏ nhất của biểu thức: Mx+y+z-3b)Cho 2 số dương x, y thỏa mãn: (sqrt{x}+1)(sqrt{y}+1)ge4.Tìm giá trị nhỏ nhất của biểu thức: Pfrac{x^2}{y}+frac{y^2}{x}
Đọc tiếp
\(a)\) Cho 3 số không âm x, y, z thỏa mãn: \(x^2+y^2+z^2=1\).
Tìm giá trị nhỏ nhất của biểu thức: \(M=x+y+z-3\)
\(b)\)Cho 2 số dương x, y thỏa mãn: \((\sqrt{x}+1)(\sqrt{y}+1)\ge4\).
Tìm giá trị nhỏ nhất của biểu thức: \(P=\frac{x^2}{y}+\frac{y^2}{x}\)
a) Từ đề bài có: \(x\left(x-1\right)\le0\Rightarrow x^2\le x\)
Tương tự hai BĐT còn lại và cộng theo vế suy ra:
\(M=x+y+z-3\ge x^2+y^2+z^2-3=-2\)
Đẳng thức xảy ra khi (x;y;z) = (0;0;1) và các hoán vị của nó
Is it true?
Đúng 0
Bình luận (0)
\(4\le\sqrt{x}+\sqrt{y}+\sqrt{xy}+1\le\sqrt{2\left(x+y\right)}+\frac{x+y}{2}+1\)
\(\Leftrightarrow\)\(8\le x+y+2\sqrt{x+y}\sqrt{2}+2=\left(\sqrt{x+y}+\sqrt{2}\right)^2\)
\(\Leftrightarrow\)\(\sqrt{x+y}+\sqrt{2}\ge\sqrt{8}\)
\(\Leftrightarrow\)\(x+y\ge\left(\sqrt{8}-\sqrt{2}\right)^2=2\)
\(\Rightarrow\)\(P=\frac{x^2}{y}+\frac{y^2}{x}\ge\frac{\left(x+y\right)^2}{x+y}=x+y\ge2\)
Dấu "=" xảy ra khi \(x=y=1\)
Đúng 0
Bình luận (0)