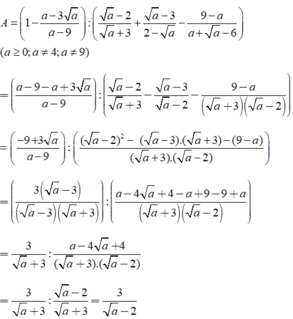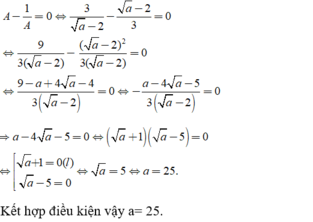Cho A=1+3+32+...+32008. Tinh 2A-32009
Những câu hỏi liên quan
Cho phép tính : 30 + 31 + 32 + 33 + ..........+ 32008 + 32009
Lấy kết quả phép tính này chia cho 8 thì số dư là bao nhiêu ?
Số số của dãy trên là:
(32009 - 30):1+1 =31980 (số)
Số cặp số của dãy là:
31980 : 2 = 15990 (cặp)
\(30+31+32+....+32008+32009\)
\(=\left(30+32009\right)+\left(31+32008\right)+...\)
\(=32039\times15990=512303610\)
Vậy \(512303610\div8=64037951\left(dư2\right)\)
Đúng 0
Bình luận (0)
1 tháng 3 2023 lúc 12:24
Cho tổng A=1+32+34+36+...+32008. Tính giá trị biểu thức: B= 8A-32010
Theo đề bài ra, ta có :
`A=1+32+34+36+....+32008`
\(\Rightarrow\) `9A = 3^2 + 3^4 + 3^6 + 3^8 + ... + 3^2010`
`9A - A=(32+34+36+38+....+ 32010)-(1+32+34+36+....+ 32008)`
\(\Rightarrow\) `8A=(-1)+32010`
\(\Rightarrow\) `8A-32010=(-1)`
@Nae
Đúng 3
Bình luận (1)
Theo đề bài ra, ta có :
A=1+3^2+3^4+3^6+....+3^2008
9A = 3^2 + 3^4 + 3^6 + 3^8 + ... + 3^2010
9A - A= (3^2+3^4+3^6+3^8+....+ 3^2010)- (1+3^2+3^4+3^6+....+ 3^2008)
8A = -1+3^2010
8A - 3^2010 = (-1)
@Nae
Đúng 2
Bình luận (0)
Bài 2:
1.Chứng minh rằng : 9999931999 - 555551997 chia hết cho 5
2.Chứng minh rằng : 1725 - 1321 + 244 Chia hết cho 10
3. Chứng minh rằng: 172008 - 112008 - 32008 + 1 chia hết cho 10
a) Ta thấy \(999993^{1999}⋮̸5\) và \(55555^{1997}⋮5\) nên \(999993^{1999}-55555^{1997}⋮̸5\), mâu thuẫn đề bài.
b)
Ta có \(17^{25}=17^{4.6+1}=17.\left(17^4\right)^6=17.\overline{A1}=\overline{B7}\) có chữ số tận cùng là 7. \(13^{21}=13^{4.5+1}=13.\left(13^4\right)^5=13.\overline{C1}=\overline{D3}\) có chữ số tận cùng là 3. \(24^4=4^4.6^4=\overline{E6}.\overline{F6}=\overline{G6}\) có chữ số tận cùng là 6 nên \(17^{25}-13^{21}+24^4\) có chữ số tận cùng là chữ số tận cùng của \(7-3+6=10\) hay là 0. Vậy \(17^{25}-13^{21}+24^4⋮10\)
c) Cách làm tương tự câu b.
Đúng 2
Bình luận (0)
CMR : Q = 1/2 x ( 72020^ 2018 - 32008^2007 ) là số nguyên chia hết cho 5
cho M=32012-32011+32010-32009
chứng minh M chia hết cho 10
Ta có: \(M=3^{2012}-3^{2011}+3^{2010}-3^{2009}\)
\(=\left(3^{2012}+3^{2010}\right)-\left(3^{2011}+3^{2009}\right)\)
\(=3^{2010}\cdot\left(3^2+1\right)-3^{2009}\left(3^2+1\right)\)
\(=\left(3^2+1\right)\cdot\left(3^{2010}-3^{2009}\right)\)
\(=10\cdot3^{2009}\cdot\left(3-1\right)⋮10\)(đpcm)
Đúng 5
Bình luận (0)
15 tháng 1 2023 lúc 10:09
cho A= 1 + 6 + 6^2 +...+ 6^32. tím số dư khi chia 2A+3 cho 37
A = 1 + 6 + 62 + ... + 632
= 1 + (6 + 62 + 63 + 64) + (65 + 66 + 67 + 68) + ... + (629 + 630 + 631 + 632)
= 1 + (62 + 1).(62 + 6) + 64(62 + 1)(62 + 6) + .... + 628(62 + 1)(62 + 6)
= 1 + (62 + 1).(62 + 6).(1 + 64 + ... + 628)
= 1 + 37. (62 + 6).(1 + 64 + ... + 628)
=> A : 37 dư 1
Khi đó 2A + 3 = 2.[1 + 37. (62 + 6).(1 + 64 + ... + 628)] + 3
= 2 + 2.37. (62 + 6).(1 + 64 + ... + 628) + 3
= 5 + 2.37. (62 + 6).(1 + 64 + ... + 628)
=> P = 2A + 3 : 37 dư 5
Đúng 2
Bình luận (0)
24 tháng 12 2021 lúc 12:10
tìm chữ số tận cùng của :
a) 32009 d) 3103
b) 22009 e) 84n+1
c) 421
giúp minh với , áp dụng đồng dư thức nha T T
Cho biểu thức
A
1
-
a
-
3
a
a
-
9
a
-
2
a
+
3...
Đọc tiếp
Cho biểu thức
A = 1 - a - 3 a a - 9 a - 2 a + 3 + a - 3 2 - a - 9 - a a + a - 6
Tìm giá trị của a để A - 1/A = 0?
A. a = 5
B. a = 3
C. a = 36
D. a = 25
a) Cho A1+3+32+33 +...+32022.Tính giá trị của biểu thức 2A - 32023b) Tìm các số nguyên x sao cho x + 10 chia hết cho x - 1 .
Đọc tiếp
a) Cho A=1+3+32+33 +...+32022.Tính giá trị của biểu thức 2A - 32023
b) Tìm các số nguyên x sao cho x + 10 chia hết cho x - 1 .
a, A = 1 + 3 + 32 + 33 +....+32022
3A = 3 + 32 + 33 +.....+32022 + 32023
3A - A = 32023 - 1
2A = 32023 - 1
2A - 22023 = 32023 - 1 - 22023
2A - 22023 = -1
b, x \(\in\) Z và x + 10 \(⋮\) x - 1 ( đk x# 1)
x + 10 \(⋮\) x - 1
\(\Leftrightarrow\) x - 1 + 11 \(⋮\) x - 1
11 \(⋮\) x - 1
x-1 \(\in\) { -11; -1; 1; 11}
x \(\in\) { -10; 0; 2; 12}
Kết luận các số nguyên x thỏa mãn yêu cầu đề bài là :
x \(\in\) { -10; 0; 2; 12}
Đúng 2
Bình luận (0)