Câu 9. Cho tam giác đều ABC có cạnh bằng 4cm . Bán kính đường tròn nội tiếp tam giác ABC bằng

Những câu hỏi liên quan
Cho tam giác đều ABC có cạnh bằng 4cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC
Bán kính đường tròn ngoại tiếp của ΔABC là:
Đúng 0
Bình luận (0)
\(R=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có cạnh bằng 4cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC
Bài 2: Cho tam giác ABC đều cạnh bằng 4cm. Tính bán kính đường tròn ngoại tiếp tam giác ABCGiúp mình giải chi tiết nhé
Bán kính đường tròn ngoại tiếp của ΔABC là:
\(R=\dfrac{a\sqrt{3}}{3}=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (1)
Cho tam giác ABC đều cạnh a nội tiếp đường tròn (O). Tính bán kính đường tròn nội tiếp tam giác ABC. A.
r
a
3
3
B.
r
a
3
2
C.
r
a
3...
Đọc tiếp
Cho tam giác ABC đều cạnh a nội tiếp đường tròn (O). Tính bán kính đường tròn nội tiếp tam giác ABC.
A. r = a 3 3
B. r = a 3 2
C. r = a 3 6
D. r = a 2 3
Chọn đáp án C.
Gọi M là trung điểm của BC: 
Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng định lí Pytago vào tam giác ABM ta có:

Đúng 0
Bình luận (0)
a)Cho tam giác ABC có các trung tuyến \(m_a=15;m_b=12;m_c=9\). Tính diện tích tam giác ABC.
b) Cho tam giác ABC đều cạnh a. Bán kính đường trọn ngoại tiếp tam giác ABC bằng?
c) Cho tam giác ABC đều cạnh 2a. Bán kính đường trọn ngoại tiếp tam giác ABC bằng?
Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng. A.
a
3
3
B.
a
3
2
C.
a
3
4
D.
a
2
2
Đọc tiếp
Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng.
A. a 3 3
B. a 3 2
C. a 3 4
D. a 2 2
Áp dụng định lí sin trong tam giác ta có a sin A = 2 R . Suy ra:
R = a 2 sin 60 ° = a 2. 3 2 = a 3 3 .
Chọn A.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A nội tiếp đường tròn (O) , cạnh bên bằng b. Tính bán kính đường tròn nội tiếp tam giác
Cho ABC là tam giác đều cạnh 6 cm. Bán kính đường tròn ngoại tiếp tam giác ABC bằng
A. 3 3
B. 2 3
C. 4 3
D. 3
Theo định lí sin trong tam giác ta có:
a sin A = 2 R ⇒ R = a 2 sin A = 6 2. sin 60 0 = 2 3
Chọn B.
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có cạnh bằng a. Hãy tính bán kính đường tròn ngoại tiếp tam giác đó.
Theo định lí sin ta có:
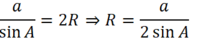
Tam giác ABC đều nên A = 60o ⇒ sin A = √3/2
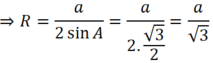
Đúng 0
Bình luận (0)












