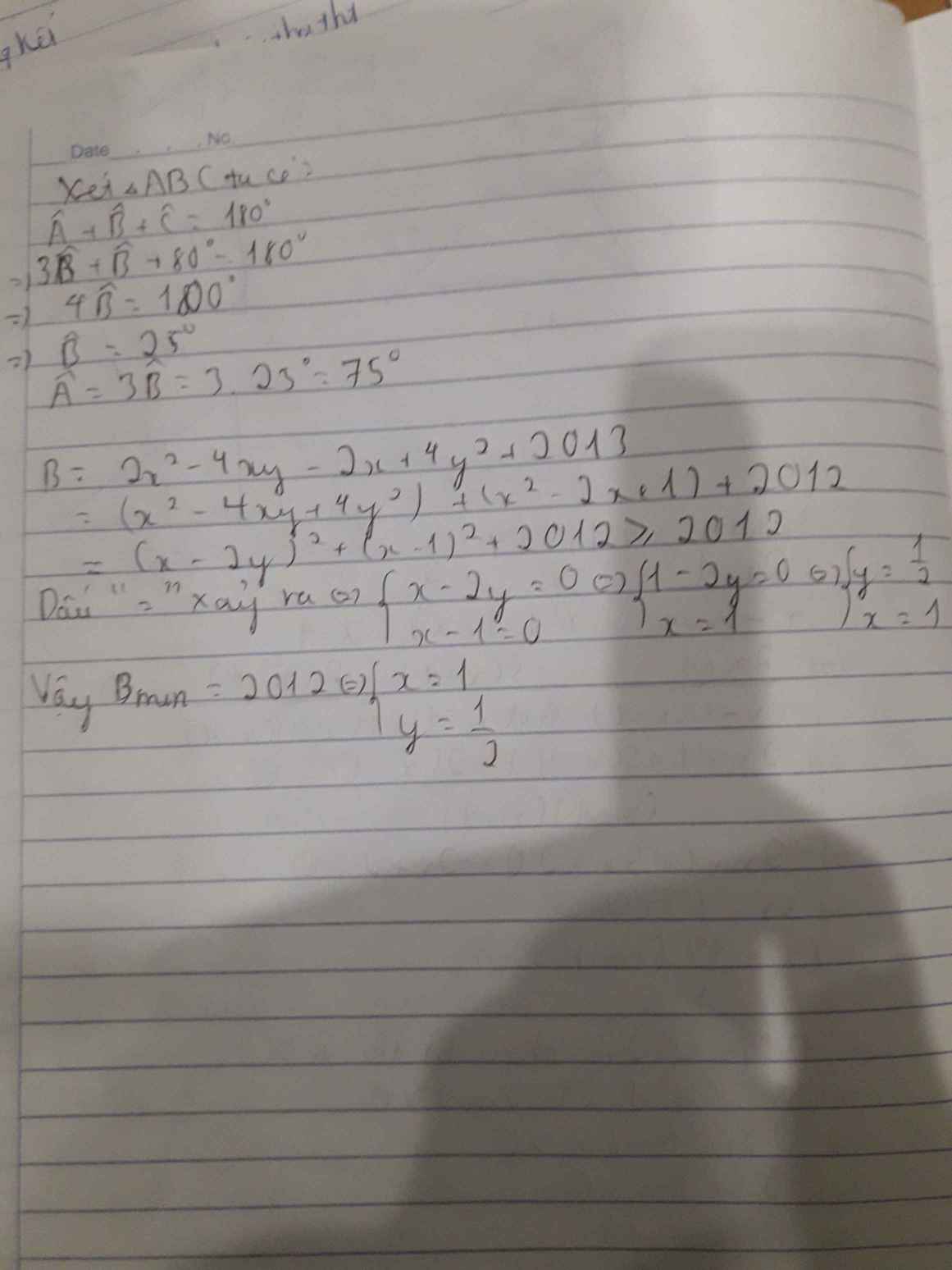Tìm giá trị nhỏ nhất của |2x + 2| + |2x - 2013|

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của biểu thức:
B=\(2x^2-4xy-2x+4y^2+2013\)
B=\(2x^2-4xy-2x+4y^2+2013\)
\(=x^2-4xy+4y^2+x^2-2x+1+2012\)
\(=\left(x-2y\right)^2+\left(x-1\right)^2+2012\ge2012\)
Dấu = xảy ra khi : \(\left(x-1\right)^2=0\Leftrightarrow x=1\)
\(\left(x-2y\right)^2=0\Leftrightarrow2y=1\Leftrightarrow y=\dfrac{1}{2}\)
Vậy \(Min_B=2012\) khi x=1 , y=\(\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
TÌM GIÁ TRỊ NHỎ NHẤT CỦA :
D=|2X-2|+|2X-2013|
Ta có:|2x-2013|=|2013-2x|
suy ra D=|2x-2|+|2013-2x|
suy ra D\(\ge\)|2x-2+2013-2x|
suy ra D\(\ge\)|-2+2013|
suy ra D\(\ge\)2011
suy ra GTNN của D là 2011 khi (2x-2)(2013-2x)
*TH1:2x-2>0\(\Rightarrow\)2x>2\(\Rightarrow\)x>1 (1)
2013-2x>0\(\Rightarrow\)2x<2013\(\Rightarrow\)x<1006.5 (2)
từ (1) và (2) \(\Rightarrow\)1<x<1006.5
*TH2:2x-2<0\(\Rightarrow\)2x<2\(\Rightarrow\)x<1 (1)
2013-2x<0\(\Rightarrow\)2x>2013\(\Rightarrow\)x>1006.5 (2)
từ (1) và (2) \(\Rightarrow\)1>x>1006.5(vô lí)
Vậy GTNN của D là 2011 khi 1<x<1006.5
Đúng 0
Bình luận (0)
giá trị nhỏ nhất là 0
vì giá trị tuyệt đối luôn lớn hơn hoặc bằng 0
Đúng 0
Bình luận (0)
Xin lỗi nha mình ghi thiếu:
suy ra GTNN của D là 2011 khi (2x-2)(2013-2x)>0
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức A=|2x-2|+|2x-2013|
ta có : A=|2x-2|+|2x-2013|
=>|2x-2|+|2x-2013| nhỏ nhất
<=> 2x-2=0 và 2x-2013=0
2x=2 2x=2013
x=1 x=2013:2=1006,5
vì 1<1006,5
=> giá trị nhỏ nhất của A = 1
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A=|2x-2|+|2x-2013| với x là số nguyên
Vì|2x-2|và|2x-2013| lớn hơn hoặc bằng 0 với mọi x thuộc R(Ko thấy kí hiệu đâu cả)
Để A nhỏ nhất suy ra tổng 2 số hạng trên nhỏ nhất
TH1: |2x-2|=0 Suy ra 2x=2=>x=1
A= 0+|2.2-2013|=2009
TH2:|2x-2013|=0=>2x=2013=>x=1006,5
A=|2x-2|+|2x-2013|=|2.1006,5-2|=2011
Vì 2011>2009 suy ra MinA =2009
Đúng 1
Bình luận (8)
Vì|2x-2|và|2x-2013| lớn hơn hoặc bằng 0 với mọi x thuộc R(Ko thấy kí hiệu đâu cả)
Để A nhỏ nhất suy ra tổng 2 số hạng trên nhỏ nhất
TH1: |2x-2|=0 Suy ra 2x=2=>x=1
A= 0+|2.2-2013|=2009
TH2:|2x-2013|=0=>2x=2013=>x=1006,5
A=|2x-2|+|2x-2013|=|2.1006,5-2|=2009
MinA =2009
Đúng 2
Bình luận (10)
Tìm giá trị nhỏ nhất của biểu thức A = |2x - 2| + |2x - 2013| với x là số nguyên
Áp dụng BĐT trị tuyệt đối ta có:
\(A=\left|2x-2\right|+\left|2x-2013\right|=\left|2x-2\right|+\left|2013-2x\right|\ge\left|2x-2+2013-2x\right|=2011\)
\(\Rightarrow A_{min}=2011\)
Dấu "=" xảy ra khi \(\left(2x-2\right)\left(2013-2x\right)\ge0\Rightarrow1\le x\le1006\)
Đúng 2
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức A=|2x-2|+|2x-2013|với x là số nguyên
vào phần câu hỏi tương tự là có đáp án nhek bn
Đúng 0
Bình luận (0)
Ta có \(A=\left|2x-2\right|+\left|2x-2013\right|=\left|2x-2\right|+\left|2013-2x\right|\)
Ta thấy \(A=\left|2x-2\right|+\left|2013-x\right|\ge\left|2x-2+2013-2x\right|=2011\) ra
Dấu " = " xảy ra khi và chỉ khi \(\left(2x-2\right).\left(2013-2x\right)\ge0\)
\(\Leftrightarrow\frac{2013}{2}\ge x\ge1\)
Vậy .....
Đúng 0
Bình luận (0)
sai rồi để A nhỏ nhất thì phải bằng 1
a,Tìm giá trị nhỏ nhất của A=(3x-2013)^2+5
b,Tìm giá trị lớn nhất của B=-(2x-8)^2-3
Tìm giá trị nhỏ nhất của
A=|2x-2|+|2x-2013| với x thuộc Z
ta có /2x-2013/=/-(2x-2013)/=/2013-2x/
/2x-2/+/2013-2x/>=/2x-2+2013-2x/
=>A>=/2011/
=>A>2011
=>A min=2011
Đúng 0
Bình luận (0)
cách khác chia khoảng: xét khoảng x=1 và x=2013/2
với x<0 ta có
A=-2x+2-2x+2013=-4x+2015 hiển nhiên x càng nhỏ A càng lớn
với 0<=0<1 A=-4x+2015 hiển nhiên A nhỏ nhất khi x tiến dần đến 1 hay A tiến dần đến 2011
với 1<=x<2013/2=> A=2x-2-2x+2013=2011 A là hằng số
với x>=2013/2=> A=2x-2+2x-2013=4x-2015 hiển nhiên x càng lớn A càng lớn GTNN khi x=2013/2=> A=2011
Đúng 0
Bình luận (0)
ta có /2x-2013/=/-(2x-2013)/=/2013-2x/
/2x-2/+/2013-2x/>=/2x-2+2013-2x/
=>A>=/2011/
=>A>2011
=>A min=2011
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của
A=|2x-2|+|2x-2013| với x thuộc Z
\(A=!2x-2!+!2x-2013!\ge!2x-2-\left(2x-2013\right)!=2011\)
đẳng thức khi (2x-2)(2x-2013)<=0 tự giải nếu cần đề bài không yêu cầu
Đúng 0
Bình luận (0)
cách khác chia khoảng: xét khoảng x=1 và x=2013/2
với x<0 ta có
A=-2x+2-2x+2013=-4x+2015 hiển nhiên x càng nhỏ A càng lớn
với 0<=0<1 A=-4x+2015 hiển nhiên A nhỏ nhất khi x tiến dần đến 1 hay A tiến dần đến 2011
với 1<=x<2013/2=> A=2x-2-2x+2013=2011 A là hằng số
với x>=2013/2=> A=2x-2+2x-2013=4x-2015 hiển nhiên x càng lớn A càng lớn GTNN khi x=2013/2=> A=2011
cách này phá trị tuyệt đối dài dòng lắm
Đúng 0
Bình luận (0)
Các bạn chú ý khi chọn lớp nhé Vì một bài toán có n! cách giải
cách giải tốt nhất là phù hợp nhất với trình độ của mình
Đúng 0
Bình luận (0)