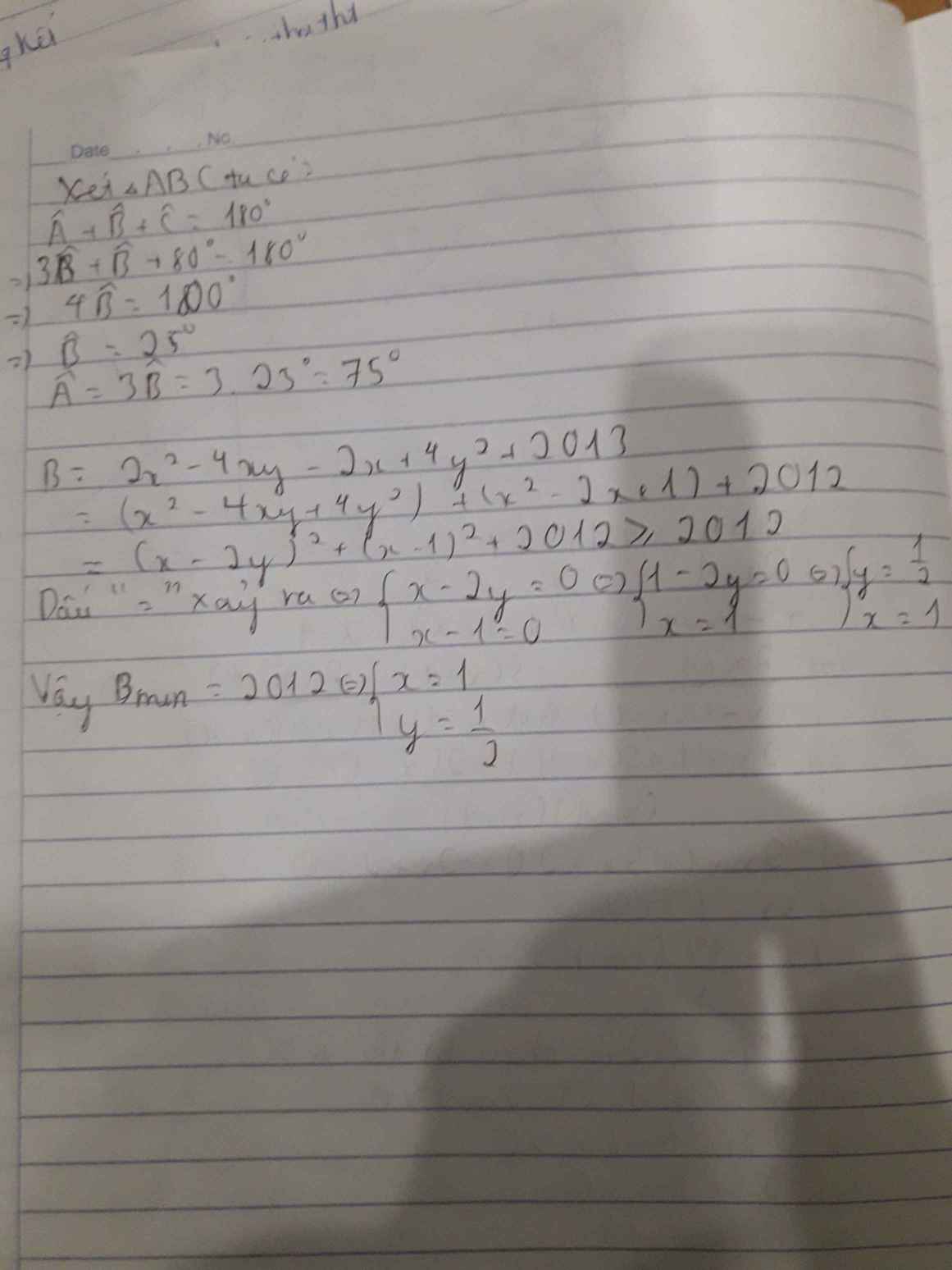B=\(2x^2-4xy-2x+4y^2+2013\)
\(=x^2-4xy+4y^2+x^2-2x+1+2012\)
\(=\left(x-2y\right)^2+\left(x-1\right)^2+2012\ge2012\)
Dấu = xảy ra khi : \(\left(x-1\right)^2=0\Leftrightarrow x=1\)
\(\left(x-2y\right)^2=0\Leftrightarrow2y=1\Leftrightarrow y=\dfrac{1}{2}\)
Vậy \(Min_B=2012\) khi x=1 , y=\(\dfrac{1}{2}\)