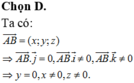Trong mặt phẳng xoy cho A (4;6) B(1;4) C(7;3/2) a tính độ dài các cạnh AB AC và BC của tam giác ABC B tính góc giữa hai vec tơ (AB BC) C chứng minh rằng tam giác ABC vuông tại A

Những câu hỏi liên quan
Trong mặt phẳng xOy, viết pt đường tròn C đường kính AB với A(-2,3) B(4,-5)
Tâm I (1;-1)
vecto IA(-3;4)
=> IA = R =\(\sqrt{3^2+4^2}=5\)
=>pt: \(\left(x-1\right)^2+\left(y+1\right)^2=25\)
Đúng 2
Bình luận (0)
Gọi phương trình đường tròn \(\left(C\right):\left(x-a\right)^2+\left(y-b\right)^2=R^2\)
Gọi \(I\) là trung điểm \(AB\)
\(\Rightarrow I\left(1;-1\right)\), đồng thời \(I\) cũng là tâm đường tròn \(\left(C\right)\)
\(R=IA=\sqrt{\left(1+2\right)^2+\left(-1-3\right)^2}=5\)
\(\Rightarrow\left(C\right):\left(x-1\right)^2+\left(y+1\right)^2=25\)
Đúng 0
Bình luận (0)
Trong mặt phẳng xOy lập phương trình đường thẳng d cách A(1;1) một khoảng bằng 2 và cách B(2;3) một khoảng bằng 4
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A và B phân biệt. Biết AB song song với mặt phẳng (zOx) và không song song với hai mặt phẳng (xOy), (yOz). Tọa độ của
A
B
⇀
có thể là (với a,b#0) A. (0;a;b) B. (a;b;0) C. (a;0;0) D. (a;0;b).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A và B phân biệt. Biết AB song song với mặt phẳng (zOx) và không song song với hai mặt phẳng (xOy), (yOz). Tọa độ của A B ⇀ có thể là (với a,b#0)
A. (0;a;b)
B. (a;b;0)
C. (a;0;0)
D. (a;0;b).
1. Cho góc xOy = 90 độ và điểm A nằm trong góc xOy gọi B và C là 2 điểm thứ tự trên Ox,Oy ( O,A thuộc nửa mặt phẳng bờ BC ) biết tam giác ABC vuông cân tại A. CMR: OA là phân giác góc xOy
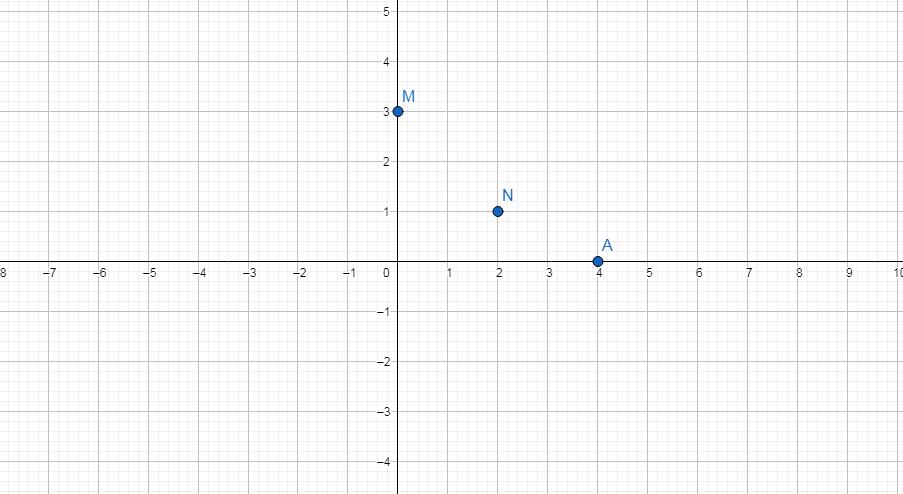
Trong 1 mặt phẳng tọa độ xoy xác định : M(03),N(21),A(40)
cho 2 góc kề bù xoy và yoz , trong đó xoy =70*
a tính yoz
b trên cùng 1 nửa mặt phẳng bờ chứa tia oy vẽ tia ot sao cho xot =120* .tính yot
a) có \(\widehat{xOy}+\widehat{yOz}=180^o\left(kb\right)\)
\(hay70^o+\widehat{yOz}=180^o\)
\(\Rightarrow\widehat{yOz}=180^o-70^o\)
\(\Rightarrow\widehat{yOz}=110^o\)
b) có \(\widehat{xOy}< \widehat{xOt}\left(70^o< 120^o\right)\)
=> Oy nằm giữa hai tia Ox và Ot
\(\Rightarrow\widehat{xOy}+\widehat{yOt}=\widehat{xOt}\)
\(hay70^o+\widehat{yOt}=120^o\)
\(\Rightarrow\widehat{yOt}=120^o-70^o\)
\(\Rightarrow\widehat{yOt}=50^o\)
Đúng 0
Bình luận (0)
cho t hỏi: Hãy vẽ các đồ thị hàm số sau lên mặt phẳng xoy (mỗi đồ thị lên 1 mặt phẳng xoy)
Tức là mỗi đồ thị vẽ riêng hay vẽ cùng 1 mp xoy z??????????
trong mặt phẳng xOy cho 3 điểm A(-1:2) B(4;-2) C(-3;-1)
tìm tọa độ của điểm M để tâm giác BCM vuông cân tại M
\(\left\{{}\begin{matrix}\overrightarrow{MB}.\overrightarrow{MC}=0\\MB=MC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[\left(x_B-x\right)\overrightarrow{i}+\left(y_B-y\right)\overrightarrow{j}\right]\left[\left(x_c-x\right)\overrightarrow{i}+\left(y_C-y\right)\overrightarrow{j}\right]=0\\\sqrt{\left(x_B-x\right)^2+\left(y_B-y\right)^2}=\sqrt{\left(x_C-x\right)^2+\left(y_C-y\right)^2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(4-x\right)\left(-3-x\right)+\left(-2-y\right)\left(-1-y\right)=0\\\left(4-x\right)^2+\left(-2-y\right)^2=\left(-3-x\right)^2+\left(-1-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-x+3y-10=0\\y+5=7x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\left(x-1\right)=0\\y=7x-5\end{matrix}\right.\)
\(\Rightarrow\)M(x;y): (0;-5) ; (1;2)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa dộ xOy, cho các điểm A(5; 4), B(2: 3) , C(6; 1)
Số đo \(\widehat{BAC}\)bằng ....
Hướng dãn cách giải hộ mình nhé !
Cho góc tù xOy. Trên nửa mặt phẳng Ox có chứa tia Oy vẽ tia Ot vuông góc Ox trên nửa mặt phẳng bờ Oy vẽ tia Oz vuông góc Oy. gọi Om là tia phân giác của xOy
a CMR Om là tia phân giác của zOt
b, tính xOy + zOt